题目内容
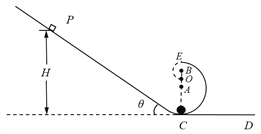
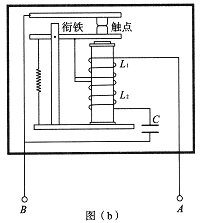
【题目】如图所示，直角坐标系xOy在竖直平面内，整个区域内有垂直于坐标系平面向外、磁感应强度为B的匀强磁场，y轴左侧还有场强为E=
、方向竖直向上的匀强电场。在第一象限内有一倾角为30°的光滑斜面。某时刻从斜面上的P点由静止释放一个质量为m、电荷量为q的小球。该小球刚好在O点处离开斜面，已知重力加速度为g。
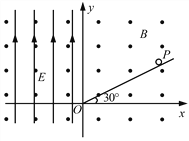
（1）求O、P两点间的距离L；
（2）求小球离y轴的最远距离xm和小球从O点至第一次打到y轴的时间t；
（3）如果在y轴上有一平板，使得小球打到平板后反弹的速度大小变为原来的
（水平分速度反向，竖直分速度方向不变）。试求小球离开O点后第N次打到y轴时的纵坐标yN以及最终打在y轴上的坐标ym。
【答案】（1）
（2）
（3）
， 
【解析】（1）小球在斜面上运动过程中受力如图1所示
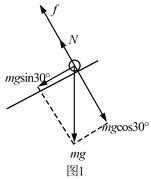
小球在O点离开斜面，即洛伦兹力大小等于重力在垂直斜面方向的分力大小，有：
qvB=mgcos 30°
此运动过程中，v2=2aL，a=gsin 30°
解得L=
（2）根据洛伦兹力方向，由左手定则可知小球带正电，小球在电场中受到的电场力大小为F=qE=mg、方向竖直向上，与重力平衡，所以小球在洛伦兹力的作用下做匀速圆周运动。轨迹如图2所示
由qvB=
可得r=
=
由几何关系有，小球离y轴的最远距离xm=(1+sin 30°)r=
运动周期T=
=
由几何关系可知，t=
=
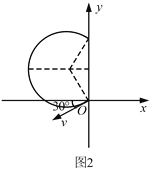
（3）由几何关系可知，小球第一次打在y轴上时的坐标为y1=
第1次小球被平板反弹后，小球的速度方向与水平方向成30°斜向左下方，再次在洛伦兹力作用下做圆周运动，轨迹如图3所示
速度大小变为原来的
，由r=可知，半径变为r1=
第2次打在y轴上时的坐标为y2=+
第N次打在y轴上时的坐标为yN=+
+…+
由等比数列求和公式可得yN=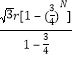
=
当N→∞时，得到最终打在y轴上的坐标ym=
