题目内容
11.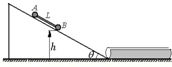 如图所示,在倾角θ=30°的光滑固定斜面上,放有质量分别为1kg和3kg的小球A和B,且两球之间用一根长L=0.3m的轻杆相连,小球B距水平面的高度h=0.3m.现让两球从静止开始自由下滑,最后都进入到上方开有细槽的光滑圆管中,不计球与圆管内壁碰撞时的机械能损失,g取10m/s2.则下列说法中正确的有( )
如图所示,在倾角θ=30°的光滑固定斜面上,放有质量分别为1kg和3kg的小球A和B,且两球之间用一根长L=0.3m的轻杆相连,小球B距水平面的高度h=0.3m.现让两球从静止开始自由下滑,最后都进入到上方开有细槽的光滑圆管中,不计球与圆管内壁碰撞时的机械能损失,g取10m/s2.则下列说法中正确的有( )| A. | 从开始下滑到A进入圆管整个过程,小球A与地球两者组成的系统机械能守恒 | |
| B. | 在B球未进入水平圆管前,小球A与地球组成系统机械能守恒 | |
| C. | 两球最后在光滑圆管中运动的速度大小为3m/s | |
| D. | 从开始下滑到A进入圆管整个过程,轻杆对B球做功1.125J |
分析 只有重力或只有弹力做功,系统机械能守恒,根据机械能守恒条件判断机械能是否守恒;以系统为研究对象,由机械能守恒定律可以求出两球最后在光滑圆管中运动的速度.以A为研究对象,应用动能定理可以求得杆对A做的功.再得到轻杆对B球做功.
解答 解:A、从开始下滑到A进入圆管整个过程,除重力做功外,杆对A做负功,小球A与地球两者组成的系统机械能不守恒,故A错误;
B、在B球未进入水平圆管前,AB一起向下的加速度为gsinθ,根据牛顿第二定律知,A、B的合力均为重力沿斜面向下的分力,杆无作用力,则对A球而言,只有重力对A做功,小球A与地球组成系统机械能守恒,故B正确;
C、以A、B组成的系统为研究对象,系统机械能守恒,由机械能守恒定律得:mBgh+mAg(h+Lsinθ)=$\frac{1}{2}$(mA+mB)v2,代入数据解得:v=$\frac{3\sqrt{3}}{2}$m/s,故C错误;
D、以A球为研究对象,由动能定理得:mAg(h+Lsinθ)+W=$\frac{1}{2}$mAv2,代入数据解得:W=-1.125J,则轻杆对B做功,WB=-W=1.1125J,故D正确;
故选:BD
点评 本题考查了求球的速度、杆做的功等问题,关键要分析两球的受力情况,明确B未进入水平管前杆是没有作用力的,分析清楚物体运动过程,应用机械能守恒定律与动能定理即可正确解题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
2.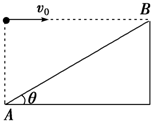 如图所示,斜面倾角为θ,位于斜面底端A正上方的小球以初速度v0正对斜面顶点B水平抛出,小球到达斜面经过的时间为t,重力加速度为g,则下列说法中正确的是( )
如图所示,斜面倾角为θ,位于斜面底端A正上方的小球以初速度v0正对斜面顶点B水平抛出,小球到达斜面经过的时间为t,重力加速度为g,则下列说法中正确的是( )
 如图所示,斜面倾角为θ,位于斜面底端A正上方的小球以初速度v0正对斜面顶点B水平抛出,小球到达斜面经过的时间为t,重力加速度为g,则下列说法中正确的是( )
如图所示,斜面倾角为θ,位于斜面底端A正上方的小球以初速度v0正对斜面顶点B水平抛出,小球到达斜面经过的时间为t,重力加速度为g,则下列说法中正确的是( )| A. | 若小球以最小位移到达斜面,则t=$\frac{2{v}_{0}cotθ}{g}$ | |
| B. | 若小球垂直击中斜面,则t=$\frac{{v}_{0}cotθ}{2g}$ | |
| C. | 若小球能击中斜面中点,则t=$\frac{2{v}_{0}cotθ}{g}$ | |
| D. | 无论小球怎样到达斜面,运动时间均为t=$\frac{2{v}_{0}tanθ}{g}$ |
16. 如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直线导线,导线中通过图示方向的恒定电流,释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中穿过线框的磁通量( )
如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直线导线,导线中通过图示方向的恒定电流,释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中穿过线框的磁通量( )
 如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直线导线,导线中通过图示方向的恒定电流,释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中穿过线框的磁通量( )
如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直线导线,导线中通过图示方向的恒定电流,释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中穿过线框的磁通量( )| A. | 逐渐增大 | |
| B. | 逐渐减小 | |
| C. | 始终为零 | |
| D. | 先增大,然后减小;在增大,最后又减小 |
3.汽车以20m/s的速度做匀速直线运动,刹车后的加速度大小为5m/s2,那么开始刹车后2s与开始刹车后6s汽车速度的大小之分别为( )
| A. | 10m/s,-10m/s | B. | 40m/s,0m/s | C. | 10m/s,0m/s | D. | 40m/s,-10m/s |
20. 两个共面共点力,F1=6N,F2=3N,F1的方向保持不变,在两个力之间的夹角θ在0°~180°变化时,关于两个力的合力,下列说法正确的是( )
两个共面共点力,F1=6N,F2=3N,F1的方向保持不变,在两个力之间的夹角θ在0°~180°变化时,关于两个力的合力,下列说法正确的是( )
 两个共面共点力,F1=6N,F2=3N,F1的方向保持不变,在两个力之间的夹角θ在0°~180°变化时,关于两个力的合力,下列说法正确的是( )
两个共面共点力,F1=6N,F2=3N,F1的方向保持不变,在两个力之间的夹角θ在0°~180°变化时,关于两个力的合力,下列说法正确的是( )| A. | 两个力的合力的最小值为3N | |
| B. | 两个力的合力可能为为8N | |
| C. | 当两个力之间的夹角为90°时,合力为3$\sqrt{10}$ N | |
| D. | 两个力的合力方向与F1方向之间的夹角的最大值为60° |
1.下列说法正确的是( )
| A. | 电路中的电流强度越大,表示通过导体截面的电量越多 | |
| B. | 各种材料的电阻率都与温度有关,金属的电阻率随温度的升高而减小 | |
| C. | 从I=U/R可知,导体中的电流跟加在它两端的电压成正比,跟它的电阻成反比 | |
| D. | 电源的电动势与外电路有关,外电路电阻越大,电动势就越大 |
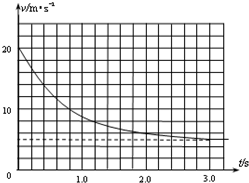 一般来说,正常人从距地面1.5m高处跳下,落地时速度较小,经过腿部的缓冲,这个速度对人是安全的,称为安全着地速度.如果人从高空跳下,必须使用降落伞才能安全着陆,其原因是,张开的降落伞受到空气对伞向上的阻力作用.经过大量实验和理论研究表明,空气对降落伞的阻力f与空气密度ρ、降落伞的迎风面积S、降落伞相对空气速度v、阻力系数c有关(由伞的形状、结构、材料等决定),其表达式是f=$\frac{1}{2}cρS{v^2}$.根据以上信息,解决下列问题.(取g=10m/s2)
一般来说,正常人从距地面1.5m高处跳下,落地时速度较小,经过腿部的缓冲,这个速度对人是安全的,称为安全着地速度.如果人从高空跳下,必须使用降落伞才能安全着陆,其原因是,张开的降落伞受到空气对伞向上的阻力作用.经过大量实验和理论研究表明,空气对降落伞的阻力f与空气密度ρ、降落伞的迎风面积S、降落伞相对空气速度v、阻力系数c有关(由伞的形状、结构、材料等决定),其表达式是f=$\frac{1}{2}cρS{v^2}$.根据以上信息,解决下列问题.(取g=10m/s2)
 如图所示,在“研究力的合成”实验中,得到了如图所示的图形,图中P为橡皮条的固定点,用两只弹簧秤或用一只弹簧秤时,都将橡皮条与细线的结点拉到O点,其中力F4是实验直接测得的合力;力F3是理论得到的合力.
如图所示,在“研究力的合成”实验中,得到了如图所示的图形,图中P为橡皮条的固定点,用两只弹簧秤或用一只弹簧秤时,都将橡皮条与细线的结点拉到O点,其中力F4是实验直接测得的合力;力F3是理论得到的合力.