题目内容
3.汽车以20m/s的速度做匀速直线运动,刹车后的加速度大小为5m/s2,那么开始刹车后2s与开始刹车后6s汽车速度的大小之分别为( )| A. | 10m/s,-10m/s | B. | 40m/s,0m/s | C. | 10m/s,0m/s | D. | 40m/s,-10m/s |
分析 根据速度公式先分析汽车静止所需要的时间,再明确给出的2s和6s时汽车的状态分析汽车是否静止,若没有静止,则根据速度公式求解,若静止则速度一定为零.
解答 解:汽车作匀减速直线运动,停止时间为:t=$\frac{v}{a}$=$\frac{20}{5}$=4s,显然刹车后2s汽车还在运动,刹车后6s,汽车已经停止,
刹车后2s的速度v1=v0+at=20-5×2=10m/s;
刹车后6s,汽车的速度为零;
故选:C.
点评 汽车刹车后将做匀减速直线运动,注意利用物理公式解题要符合实际情况,不能像数学运算一样,如在本题中,要注意判断汽车在所给时间内是否已经停止,这点是学生容易出错的地方.

练习册系列答案
相关题目
13.关于电源的电动势ε,说法错误的是( )
| A. | 电动势ε等于闭合电路中内、外电压之和 | |
| B. | 电动势ε表示该电源把其他形式的能转化为电能的本领大小 | |
| C. | 外电路断开时的外电压U=0 | |
| D. | 外电路断开时,电源的电动势已不存在了 |
11.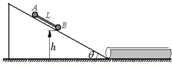 如图所示,在倾角θ=30°的光滑固定斜面上,放有质量分别为1kg和3kg的小球A和B,且两球之间用一根长L=0.3m的轻杆相连,小球B距水平面的高度h=0.3m.现让两球从静止开始自由下滑,最后都进入到上方开有细槽的光滑圆管中,不计球与圆管内壁碰撞时的机械能损失,g取10m/s2.则下列说法中正确的有( )
如图所示,在倾角θ=30°的光滑固定斜面上,放有质量分别为1kg和3kg的小球A和B,且两球之间用一根长L=0.3m的轻杆相连,小球B距水平面的高度h=0.3m.现让两球从静止开始自由下滑,最后都进入到上方开有细槽的光滑圆管中,不计球与圆管内壁碰撞时的机械能损失,g取10m/s2.则下列说法中正确的有( )
 如图所示,在倾角θ=30°的光滑固定斜面上,放有质量分别为1kg和3kg的小球A和B,且两球之间用一根长L=0.3m的轻杆相连,小球B距水平面的高度h=0.3m.现让两球从静止开始自由下滑,最后都进入到上方开有细槽的光滑圆管中,不计球与圆管内壁碰撞时的机械能损失,g取10m/s2.则下列说法中正确的有( )
如图所示,在倾角θ=30°的光滑固定斜面上,放有质量分别为1kg和3kg的小球A和B,且两球之间用一根长L=0.3m的轻杆相连,小球B距水平面的高度h=0.3m.现让两球从静止开始自由下滑,最后都进入到上方开有细槽的光滑圆管中,不计球与圆管内壁碰撞时的机械能损失,g取10m/s2.则下列说法中正确的有( )| A. | 从开始下滑到A进入圆管整个过程,小球A与地球两者组成的系统机械能守恒 | |
| B. | 在B球未进入水平圆管前,小球A与地球组成系统机械能守恒 | |
| C. | 两球最后在光滑圆管中运动的速度大小为3m/s | |
| D. | 从开始下滑到A进入圆管整个过程,轻杆对B球做功1.125J |
8.下列关于电场线和磁感线的说法中,正确的是( )
| A. | 电流与电流之间的相互作用一定是通过磁场来发生的 | |
| B. | 磁场中两条磁感线一定不相交,但在复杂电场中的电场线是可以相交的 | |
| C. | 电场线和磁感线都是电场或磁场中实际存在的线 | |
| D. | 磁感线分布较密的地方,同一试探电荷所受的磁场力也越大 |
15.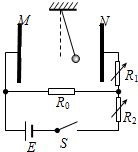 如图所示,M、N是平行板电容器的两个极板,R0为定值电阻,R1、R2为可调电阻,用绝缘细线将质量为m、带正电的小球悬于电容器内部.闭合电键S,小球静止时受到悬线的拉力为F.调节R1、R2,关于F的大小判断正确的是( )
如图所示,M、N是平行板电容器的两个极板,R0为定值电阻,R1、R2为可调电阻,用绝缘细线将质量为m、带正电的小球悬于电容器内部.闭合电键S,小球静止时受到悬线的拉力为F.调节R1、R2,关于F的大小判断正确的是( )
 如图所示,M、N是平行板电容器的两个极板,R0为定值电阻,R1、R2为可调电阻,用绝缘细线将质量为m、带正电的小球悬于电容器内部.闭合电键S,小球静止时受到悬线的拉力为F.调节R1、R2,关于F的大小判断正确的是( )
如图所示,M、N是平行板电容器的两个极板,R0为定值电阻,R1、R2为可调电阻,用绝缘细线将质量为m、带正电的小球悬于电容器内部.闭合电键S,小球静止时受到悬线的拉力为F.调节R1、R2,关于F的大小判断正确的是( )| A. | 保持R1不变,缓慢增大R2时,F将变小 | |
| B. | 保持R1不变,缓慢增大R2时,F将不变 | |
| C. | 保持R2不变,缓慢增大R1时,F将变小 | |
| D. | 保持R2不变,缓慢增大R1时,F将不变 |
12.如图所示,光滑的水平地面上有20块木块1、2、3、…20,第1、3、5…块质量均为m,第2、4、6…块质量均为2m,现用力F向右推第一块木块,则第15块木块对第14块木块的弹力大小为( )

| A. | $\frac{3}{10}$F,向左 | B. | $\frac{3}{7}$F,向左 | C. | $\frac{4}{15}$F,向右 | D. | $\frac{7}{30}$F,向右 |
13.完全相同的两辆汽车,都拖着完全相同的拖车(与汽车质量相等)以相同的速度在平直公路上以速度v匀速齐头并进,汽车与拖车的质量均为m,某一时刻两拖车同时与汽车脱离之后,甲汽车保持原来的牵引力继续前进,乙汽车保持原来的功率继续前进,经过一段时间后甲车的速度变为2v,乙车的速度变为1.5v,若路面对汽车的阻力恒为车重的0.1倍,取g=10m/s2,则此时( )
| A. | 甲乙两车在这段时间内的位移之比为4:3 | |
| B. | 甲车的功率增大到原来的4倍 | |
| C. | 甲乙两车在这段时间内克服阻力做功之比为12:11 | |
| D. | 甲乙两车在这段时间内牵引力做功之比为3:2 |