题目内容
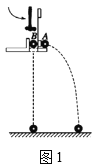
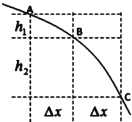
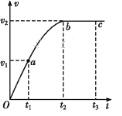
【题目】间距为l=0.5m两平行金属导轨由倾斜部分和水平部分平滑连接而成，如图所示，倾斜部分导轨的倾角θ=30°，上端连有阻值R=0.5Ω的定值电阻且倾斜导轨处于大小为B1=0.5T、方向垂直导轨平面向上的匀强磁场中。水平部分导轨足够长，图示矩形虚线框区域存在大小为B2=1T、方向竖直向上的匀强磁场，磁场区域的宽度d=3m。现将质量m=0.1kg、内阻r=0.5Ω、长l=0.5m的导体棒ab从倾斜导轨上端释放，达到稳定速度v0后进入水平导轨，当恰好穿过B2磁场时速度v=2m/s，已知导体棒穿过B2磁场的过程中速度变化量与在磁场中通过的距离满足
（比例系数k未知），运动过程中导体棒始终与导轨垂直并接触良好，不计摩擦阻力和导轨电阻。求：
（1）导体棒ab的速度v0；
（2）导体棒ab穿过B2磁场过程中通过R的电荷量及导体棒ab产生的焦耳热；
（3）若磁场B1大小可以调节，其他条件不变，为了使导体棒ab停留在B2磁场区域，B1需满足什么条件。
【答案】（1）8m/s（2）1.5C;1.5J（3）
【解析】
（1）当导体棒ab运动稳定后做匀速运动，由平衡条件和安培力公式结合求解导体棒ab的速度v0；
（2）通过R的电荷量可根据电量与电流的关系、欧姆定律和法拉第电磁感应定律结合求解。由能量守恒定律和能量分配关系求导体棒ab产生的焦耳热；
（3）当导体棒ab在B2磁场区域通过的位移x'＜d时棒ab将停留在B2磁场区域。根据题意求出k，从而得到导体棒ab以速度v′通过B2磁场时与在磁场中通过的距离x′满足的关系，再结合导体棒ab在B1磁场中达到稳定速度受力平衡列式求解。
（1）当导体棒ab运动稳定后，做匀速运动，由平衡条件知，
感应电流
联立得
（2）穿过B2磁场过程中的平均电流：
联立得
=
1.5C
设穿过B2磁场过程中产生的总焦耳热为Q，则由能量守恒定律知
导体棒ab产生的焦耳热
联立得Q=1.5 J
（3）根据题意有， 
，则若导体棒ab以速度v′通过B2磁场时与在磁场中通过的距离x′满足
导体棒ab在B1磁场中达到稳定速度时，由平衡条件知
又
联立得
根据题意， 
联立以上二式并代入数据得
。
