题目内容
17.一行星绕恒星作圆周运动.由天文观测可得,其运行周期为T,速度为v,引力常量为G,则下列说法错误的是( )| A. | 恒星的质量为$\frac{{v}^{3}T}{2πG}$ | B. | 行星的质量为$\frac{4{π}^{2}{v}^{3}}{2πG}$ | ||
| C. | 行星运动的轨道半径为$\frac{vT}{2π}$ | D. | 行星运动的加速度为$\frac{2πv}{T}$ |
分析 根据圆周运动知识和已知物理量求出轨道半径和加速度.根据万有引力提供向心力,列出等式求出中心体的质量.
解答 解:C、根据圆周运动知识得:
由v=$\frac{2πr}{T}$得:行星运动的轨道半径为 r=$\frac{vT}{2π}$ ①
故C正确.
A、根据万有引力提供向心力,列出等式:G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r ②
由①②得恒星的质量 M=$\frac{{v}^{3}T}{2πG}$,故A正确;
B、由上式知,无法求出行星的质量,故B错误.
D、行星运动的加速度 a=$\frac{{v}^{2}}{r}$=ωv=$\frac{2πv}{T}$,故D正确.
本题选错误的,故选:B.
点评 本题考查万有引力与圆周运动问题.根据万有引力提供向心力,列出等式可求出中心体的质量,不能求出环绕体质量.

练习册系列答案
相关题目
8. 2007年10月24日,我国首次成功发射了探月卫星-“嫦娥一号”.卫星在地月转移轨道飞赴月球的过程中,与地球间距增大,与月球间距减小,则( )
2007年10月24日,我国首次成功发射了探月卫星-“嫦娥一号”.卫星在地月转移轨道飞赴月球的过程中,与地球间距增大,与月球间距减小,则( )
 2007年10月24日,我国首次成功发射了探月卫星-“嫦娥一号”.卫星在地月转移轨道飞赴月球的过程中,与地球间距增大,与月球间距减小,则( )
2007年10月24日,我国首次成功发射了探月卫星-“嫦娥一号”.卫星在地月转移轨道飞赴月球的过程中,与地球间距增大,与月球间距减小,则( )| A. | 地球对它的万有引力增大,月球对它的万有引力减小 | |
| B. | 地球对它的万有引力减小,月球对它的万有引力增大 | |
| C. | 地球和月球对它的万有引力均不变 | |
| D. | 当它绕月球运动时,不再受地球万有引力的作用 |
12.下列说法中错误的是( )
| A. | 比结合能越小,原子核越稳定 | |
| B. | 天然放射现象的发现,揭示了原子的核式结构 | |
| C. | γ射线是波长很短的电磁波,它的穿透能力比β射线要强 | |
| D. | 氡的半衰期为3.8天,某矿石中有10个氡原子核,经过3.8天,此矿石中只剩下5个氡原子核 | |
| E. | 玻尔是第一个把微观世界中物理量取分立值的观念应用到原子系统的科学家 |
9.下列属于电场强度E单位的是( )
| A. | V/m | B. | J/C | C. | N/C | D. | C/V |
6.物体做自由落体运动,Ek表示物体的动能,Ep表示重力势能,h表示物体下落的距离,v表示物体运动的速度,t表示物体运动的时间,以水平地面为零势能面.下列图象中,能正确反映各物理量之间关系的是( )
| A. |  | B. |  | C. | 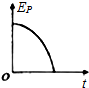 | D. |  |
7.分析研究下列物体的运动时,研究对象能看做质点的是( )
| A. | 研究“嫦娥三号”“奔月”的过程 | |
| B. | 研究奥运冠军邓琳琳在平衡木上的动作 | |
| C. | 研究从斜面上滑下的木块的滑行时间 | |
| D. | 研究运动员发出的弧旋乒乓球的旋转情况 |
