题目内容
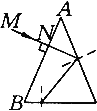
【题目】质谱仪是利用电场和磁场分析带电粒子性质的仪器,某同学设计的一种质谱仪结构如图所示。一对平行金属板的板间距为![]() ,板间电压为
,板间电压为![]() ,上极板带正电。我们把板间区域叫区域Ⅰ。在上板右端紧挨着上板垂直放置一足够大的荧光屏
,上极板带正电。我们把板间区域叫区域Ⅰ。在上板右端紧挨着上板垂直放置一足够大的荧光屏![]() 。以下板右端点
。以下板右端点![]() 为顶点的足够大的区域
为顶点的足够大的区域![]() 叫做区域Ⅱ,角
叫做区域Ⅱ,角![]() 。在区域Ⅰ、Ⅱ间均分布有垂直纸面向里,磁感应强度为
。在区域Ⅰ、Ⅱ间均分布有垂直纸面向里,磁感应强度为![]() 的匀强磁场。以下问题中均不考虑带电粒子的重力和带电粒子之间的相互作用。
的匀强磁场。以下问题中均不考虑带电粒子的重力和带电粒子之间的相互作用。
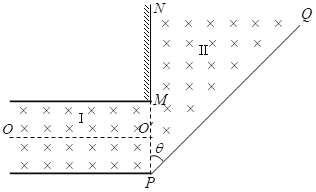
(1)某带电粒子沿两板间中线![]() 方向射入后沿直线运动进入区域Ⅱ,恰好垂直
方向射入后沿直线运动进入区域Ⅱ,恰好垂直![]() 边界射出,判断带电粒子的电性,求出粒子的荷质比以及粒子在区域Ⅱ中的运动时间;
边界射出,判断带电粒子的电性,求出粒子的荷质比以及粒子在区域Ⅱ中的运动时间;
(2)仅将(1)问中的粒子电性改变,而且将大量这样的粒子从两极板左端口从上到下均匀排列,沿平行极板方向源源不断地射入板间。求某时刻击中荧光屏的粒子个数与它们射入极板间时射入总数的比;
(3)在(2)问中若屏上某点接收到粒子流形成的电流为![]() ,假设粒子击中屏后速度变为零,求粒子对屏的平均撞击力大小。
,假设粒子击中屏后速度变为零,求粒子对屏的平均撞击力大小。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)粒子恰好垂直![]() 边界射出,根据左手定则可知粒子在带负电;
边界射出,根据左手定则可知粒子在带负电;
粒子区域Ⅰ中做匀速直线运动,则有:
![]()
![]()
设粒子在区域Ⅱ中做圆周运动的轨迹半径为![]() ,如图所示,由几何关系得:
,如图所示,由几何关系得:
![]()
根据牛顿第二定律可得:
![]()
联立解得粒子的荷质比为:
![]()
设粒子在区域Ⅱ中做圆周运动的周期为:
![]()
由几何关系得圆心角为![]() ,粒子在区域Ⅱ中的运动时间:
,粒子在区域Ⅱ中的运动时间:
![]()

(2)设从![]() 点射入区域Ⅱ的粒子在区域Ⅱ中运动的轨迹恰好与边界
点射入区域Ⅱ的粒子在区域Ⅱ中运动的轨迹恰好与边界![]() 相切,如图所示。
相切,如图所示。
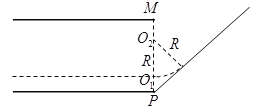
由题目已知可得,粒子轨迹半径仍为![]() ,则在
,则在![]() 之间射入区域Ⅱ的粒子均可以击中荧光屏,设轨迹圆的圆心为
之间射入区域Ⅱ的粒子均可以击中荧光屏,设轨迹圆的圆心为![]() ,则有:
,则有:
![]()
![]()
![]()
击中荧光屏的粒子个数与它们射入极板间时射入总数的比:
![]()
(3)设一段短时间![]() 内击中荧光屏上某点的粒子个数为
内击中荧光屏上某点的粒子个数为![]() ,根据动量定理有:
,根据动量定理有:
![]()
根据电流定义可有:
![]()
解得:
![]()
由牛顿第三定律知,粒子对屏的平均撞击力大小为:
![]()

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】某物理小组的同学设计了一个小钢球通过凹形桥最低点时的速度的实验。所用器材有:小钢球、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为![]() )。请完成下列填空:
)。请完成下列填空:
(1)将凹形桥模拟器静置于托盘秤上,如图(a)所示,托盘秤的示数为![]() ;
;
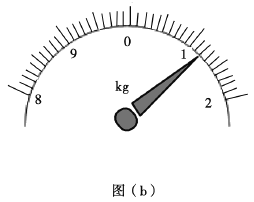
(2)将小钢球静置于凹形桥模拟器最低点时,托盘秤的示数如图(b)所示,该示数为________kg;

(3)将小钢球从凹形桥模拟器某一位置释放,小钢球经过最低点后滑向另一侧,此过程中托盘秤的最大示数为m;多次从同一位置释放小钢球,记录各次的m值如下表所示:
序号 | 1 | 2 | 3 | 4 | 5 |
| 2.3 | 2.2 | 2.3 | 2.1 | 2.0 |
(4)根据以上数据,可求出小钢球经过凹形桥最低点时对桥的压力为________N;小钢球通过最低点时的速度大小为________![]() (重力加速度大小取
(重力加速度大小取![]() ,速度计算结果保留2位有效数字)。
,速度计算结果保留2位有效数字)。