题目内容
16.某同学想测量一合金制成的圆柱体的电阻率.(1)现用螺旋测微器测量该圆柱体的直径,用游标卡尺测量该圆柱体的长度.螺旋测微器和游标卡尺的示数如图(a)和图(b)所示.由图读得圆柱体的直径为D=1.845mm,长度为L=4.240cm.
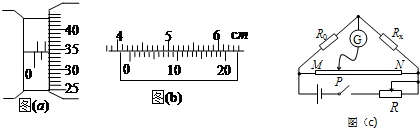
(2)由于缺乏仪器,该同学用图(c)所示的电路来测量圆柱体的阻值.图中Rx是待测圆柱体,R0是定值电阻,G是灵敏度很高的电流表,MN是一段均匀的电阻丝.闭合开关,改变滑动头P的位置,当通过电流表G的电流为零时,测得MP=x1,PN=x2,则Rx的阻值为$\frac{{x}_{2}}{{x}_{1}}$R0.该圆柱体的电阻率的关系式为ρ=$\frac{π{D}^{2}{R}_{0}{x}_{2}}{{4Lx}_{1}}$.(用字母表示),若流经圆柱体的电流为I,圆柱体两端之间的电压为U,圆柱体的直径和长度分别用D、L表示,则用D、L、I、U表示的$\frac{π{D}^{2}U}{4IL}$.
分析 (1)螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数;游标卡尺主尺与游标尺示数之和是游标卡尺的示数.
(2)闭合开关,改变滑动头P的位置,当通过电流表G的电流为零时,说明通过电阻丝两侧的电流是相等的,而总电流一定,故通过R0和Rx的电流也相等;并联电路电压相等,故电阻丝MP段与PN段电压之比等于R0和Rx的电压比;再结合电阻定律列式求解即可;应用电阻定律与欧姆定律可以求出电阻率的表达式.
解答 解:(1)由图示螺旋测微器可知,其示数:D=1.5mm+34.5×0.01mm=1.845mm;
由图示游标卡尺可知,其示数:42mm+8×0.05mm=42.40mm=4.240cm;
(2)电阻丝MP段与PN段电压之比等于R0和Rx的电压比,即$\frac{{U}_{MP}}{{U}_{PN}}$=$\frac{{U}_{R0}}{{U}_{RX}}$=$\frac{{R}_{0}}{{R}_{X}}$,
通过电流表G的电流为零,说明通过电阻丝两侧的电流是相等的,而总电流一定,
故通过R0和Rx的电流也相等,故$\frac{{R}_{MP}}{{R}_{PN}}$=$\frac{{R}_{0}}{{R}_{X}}$,根据电阻定律:R=ρ$\frac{L}{S}$可知:$\frac{{R}_{MP}}{{R}_{PN}}$=$\frac{{x}_{1}}{{x}_{2}}$,
故:$\frac{{R}_{0}}{{R}_{X}}$=$\frac{{x}_{1}}{{x}_{2}}$,解得:RX=$\frac{{x}_{2}}{{x}_{1}}$R0;圆柱体的电阻:RX=ρ$\frac{L}{S}$=ρ$\frac{L}{π(\frac{D}{2})^{2}}$,则电阻率:ρ=$\frac{π{D}^{2}{R}_{0}{x}_{2}}{{4Lx}_{1}}$;
若流经圆柱体的电流为I,圆柱体两端之间的电压为U,圆柱体的电阻:RX=$\frac{U}{I}$,
由电阻定律可知:RX=ρ$\frac{L}{S}$=ρ$\frac{L}{π(\frac{D}{2})^{2}}$,电阻率:ρ=$\frac{π{D}^{2}U}{4IL}$;
故答案为:(1)1.845;4.240;(2)$\frac{{x}_{2}}{{x}_{1}}$R0;$\frac{π{D}^{2}{R}_{0}{x}_{2}}{{4Lx}_{1}}$;$\frac{π{D}^{2}U}{4IL}$.
点评 本题考查了螺旋测微器与游标卡尺读数、考查了电桥法测电阻实验,要掌握常用器材的使用及读数方法,螺旋测微器需要估读,游标卡尺不需要估读,对游标卡尺读数时要注意游标尺的精度.

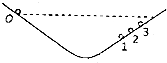 伽利略创造的把实验、假设和逻辑锥理相结合的科学方法,有力地促进了人类科学认设的发展,利用如图所示的装置做如下实验;小球从左侧斜面上的O点由静止释放后沿斜面向下运动,并沿右侧斜面上升.斜面上先后铺垫三种粗糙程度逐渐降低的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3,根据三次实验结果的对比,可以得到的最直接的结论是( )
伽利略创造的把实验、假设和逻辑锥理相结合的科学方法,有力地促进了人类科学认设的发展,利用如图所示的装置做如下实验;小球从左侧斜面上的O点由静止释放后沿斜面向下运动,并沿右侧斜面上升.斜面上先后铺垫三种粗糙程度逐渐降低的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3,根据三次实验结果的对比,可以得到的最直接的结论是( )| A. | 如果小球受力的作用,它的运动状态将发生改变 | |
| B. | 如果小球不受力,它将一直保持匀速运动或静止状态 | |
| C. | 如果斜面光滑,小球将上升到与O点等高的位置 | |
| D. | 小球受到的力一定时,质量越大,它的加速度越小 |
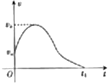 如图所示为带电粒子只在电场力作用下运动的v-t图象,在a点的速度为va,运动到b点的速度为vb.则下列说法中正确的是( )
如图所示为带电粒子只在电场力作用下运动的v-t图象,在a点的速度为va,运动到b点的速度为vb.则下列说法中正确的是( )| A. | 电场中a点电势一定比b点电势高 | |
| B. | 粒子在a点的电势能一定比在b点的电势能大 | |
| C. | 在0~t1时间内,粒子运动路径与电场力可能不在一条直线上 | |
| D. | 在0~t2时间内,粒子运动过程中受到的电场力先减小后增大 |
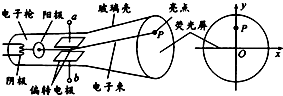 如图所示为阴极射线管的结构示意图,从阴极脱离出来的电子经阴极和阳极之间的加速电场加速后通过阳极上的小孔.然后在偏转电极间电场作用下发生偏转并最终打在荧光屏上形成亮点P.关于阴极射线管的工作原理,下列说法正确的是
如图所示为阴极射线管的结构示意图,从阴极脱离出来的电子经阴极和阳极之间的加速电场加速后通过阳极上的小孔.然后在偏转电极间电场作用下发生偏转并最终打在荧光屏上形成亮点P.关于阴极射线管的工作原理,下列说法正确的是( )
| A. | 当偏转电极的电势φa<φb时,电子流将可能沿图示径迹运动并在荧光屏上形成亮点P | |
| B. | 若只增加阴极和阳极间的加速电压,亮点P将沿y轴远离荧光屏中心O | |
| C. | 若只减小偏转电极间的电压,亮点P将沿y轴靠近荧光屏中心O | |
| D. | 若只增加偏转电极间的电压,电子从阴极出发运动到荧光屏的时间将增长 |
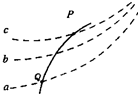 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q 是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q 是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最高 | |
| B. | 带电质点通过 P 点时电势能较小 | |
| C. | 带电质点通过 P 点时的动能较大 | |
| D. | 带电质点通过 P 点时的加速度较大 |
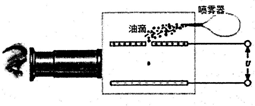 美国物理学家密立根所做的油滴实验在近代物理学发展中占有非常重要的地位,该实验清楚的证明了电荷的颗粒性,并确定了最小单位电荷的量值.密立根油滴实验的原理示意图如图所示,两块平行金属板水平放置,上板带正电,下板带负电,板间距为d,上板开有一小孔,喷雾器喷出大小不同的带电油滴,经上板小孔进入两板间,现调节两板间电压为U,通过左侧的显微装置观测到一质量为m的带电油滴恰好静止在两板正中央,忽略空气阻力和浮力,两板间电场视为匀强电场,元电荷的电量为e,重力加速度为g.
美国物理学家密立根所做的油滴实验在近代物理学发展中占有非常重要的地位,该实验清楚的证明了电荷的颗粒性,并确定了最小单位电荷的量值.密立根油滴实验的原理示意图如图所示,两块平行金属板水平放置,上板带正电,下板带负电,板间距为d,上板开有一小孔,喷雾器喷出大小不同的带电油滴,经上板小孔进入两板间,现调节两板间电压为U,通过左侧的显微装置观测到一质量为m的带电油滴恰好静止在两板正中央,忽略空气阻力和浮力,两板间电场视为匀强电场,元电荷的电量为e,重力加速度为g.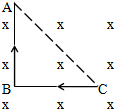 长为2L导线,AC对折成直角,放在磁感强度为B的匀强磁场中,如图所示,当导线中通以电流I时所受安培力为$\sqrt{2}$BIL,若导线ABC构成闭合回路,所受安培力变为0.
长为2L导线,AC对折成直角,放在磁感强度为B的匀强磁场中,如图所示,当导线中通以电流I时所受安培力为$\sqrt{2}$BIL,若导线ABC构成闭合回路,所受安培力变为0.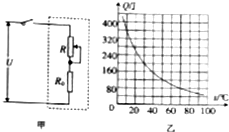 图甲是一种家用电熨斗的电路原理图(额定电压为220V),虚线框内为加热电路,R0是定值电阻,R是可变电阻.当该电熨斗所接电压为其额定电压时,该电熨斗的最低耗电功率为100W,最高耗电功率为500W.
图甲是一种家用电熨斗的电路原理图(额定电压为220V),虚线框内为加热电路,R0是定值电阻,R是可变电阻.当该电熨斗所接电压为其额定电压时,该电熨斗的最低耗电功率为100W,最高耗电功率为500W.