题目内容
17．
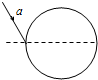如图所示，是一种透明材料作成的圆柱形物体的横截面．一细束激光a沿着该横截面，以60°的入射角，从真空射入该圆柱形物体．已知这种材料的折射率为n=$\sqrt{3}$．假设激光是从透明圆柱体的最左端射入圆球的，则从该截面中能射出激光束的（ ）| A． | 只有1处 | B． | 只有2处 | C． | 只有3处 | D． | 可能有4处 |
分析 根据折射定律求出光线在透明圆柱体中的折射角，判断是否发生全反射，再结合折射定律分析判断．
解答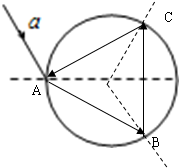 
解：根据折射定律得：$\frac{sin60°}{sinα}=n=\sqrt{3}$，
解得光线在A点进入圆柱体后折射角α=30°，
根据几何关系知，光线在B点的入射角为30°，
由于sin30°＜sinC=$\frac{1}{n}=\frac{\sqrt{3}}{3}$，可知光线在B点不会发生全反射，在B点有折射也有反射，同理在C点有折射也有反射．
由图可知，从该截面能射出的激光束有3处．
故选：C．
点评 本题考查了折射定律的基本运用，知道光线发生全反射的条件，注意入射角和临界的关系，运用几何关系进行求解．
练习册系列答案
相关题目
8．
a、b、c是三个相同的粒子，且均带正电，由同一点同时垂直电场方向进入偏转电场，其轨迹如图所示，其中b恰好从下极板边缘飞出电场．粒子重力不计．由此可以确定（ ）
a、b、c是三个相同的粒子，且均带正电，由同一点同时垂直电场方向进入偏转电场，其轨迹如图所示，其中b恰好从下极板边缘飞出电场．粒子重力不计．由此可以确定（ ）| A． | 在b飞离电场的同时，a刚好打在负极板上 | |
| B． | b和c同时飞离电场 | |
| C． | 进入电场时，c的速度最大，a的速度最小 | |
| D． | 在两板间运动的过程中，电势能的减少量，c最小，a和b一样大 |
12．上海锦江乐园新建的“摩天转轮”，它的直径达98m，世界排名第五．游人乘坐时，转轮始终不停地匀速转动，每转一周用时25min，下列说法中正确的是（ ）
| A． | 每时每刻，每个乘客受到的合力都不等于零 | |
| B． | 每个乘客都在做加速度为零的匀速运动 | |
| C． | 乘客在乘坐过程中对座位的压力始终不变 | |
| D． | 乘客运动的加速度始终保持不变 |
9．
a、b、c、d是匀强电场中的四个点，它们正好是一个平行四边形的四个顶点，电场线与平行四边形所在平面平行．已知a点的电势为11V，b点的电势为13V，c点的电势为15V，如图，由此可知d点的电势为（ ）
a、b、c、d是匀强电场中的四个点，它们正好是一个平行四边形的四个顶点，电场线与平行四边形所在平面平行．已知a点的电势为11V，b点的电势为13V，c点的电势为15V，如图，由此可知d点的电势为（ ）| A． | 11V | B． | 13V | C． | 15V | D． | 17V |
6．如图，一束α粒子沿中心轴射入两平行金属板之间的匀强电场中后，分成三束a、b、c，则（ ）
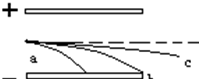
| A． | 初速度比较va＜vb＜vc | B． | 板内运动时间比较ta=tb＜tc | ||
| C． | 电势能的变化量比较△Pa＞△Pb＞△Pc | D． | 动能增加量比较△Eka＞△Ekb＞△Ekc |
3．
如图所示，虚线a、b、c表示O处点电荷的电场中的三个等势面，设两相邻等势面的间电势差相等．一电子（不计重力）射入电场后的运动轨迹如图中实线所示，其中1、2、3、4表示运动轨迹与等势面的一些交点．由此可以判定（ ）
如图所示，虚线a、b、c表示O处点电荷的电场中的三个等势面，设两相邻等势面的间电势差相等．一电子（不计重力）射入电场后的运动轨迹如图中实线所示，其中1、2、3、4表示运动轨迹与等势面的一些交点．由此可以判定（ ）| A． | O处的点电荷一定带正电 | |
| B． | a、b、c三个等势面的电势关系是φa＜φb＜φc | |
| C． | 电子从位置1到2和从位置3到4的过程中电场力做功的关系是|W12|=2|W34| | |
| D． | 电子在1、2、3、4四个位置各处具有的电势能与动能的总和相等 |