题目内容
6.如图,一束α粒子沿中心轴射入两平行金属板之间的匀强电场中后,分成三束a、b、c,则( )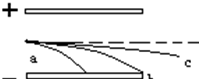
| A. | 初速度比较va<vb<vc | B. | 板内运动时间比较ta=tb<tc | ||
| C. | 电势能的变化量比较△Pa>△Pb>△Pc | D. | 动能增加量比较△Eka>△Ekb>△Ekc |
分析 α粒子在匀强电场中做类平抛运动,将a与b,b与c进行比较,可得到时间关系和初速度的关系;根据电场力做功,比较电势能变化量的关系;根据动能定理列式比较动能增加量的关系.
解答 解:AB、α粒子在匀强电场中加速度不变.沿垂直于极板的方向,受到电场力作用而初速度为零的匀加速直线运动,平行于极板的方向不受力而做匀速直线运动.
垂直于极板的方向:由y=$\frac{1}{2}a{t}^{2}$知,t=$\sqrt{\frac{2y}{a}}$∝$\sqrt{y}$,由于ya=yb>yc,则得:ta=tb>tc.
平行于极板的方向,有:x=v0t,得:v0=$\frac{x}{t}$
对于a、b:由于xa<xb,ta=tb,则得:va<vb.
对于b、c:xb=xc,tb>tc.则得,vb<vc.故有较va<vb<vc.故A正确,B错误.
C、电势能的变化量大小等于电场力做功的大小,则△Pp=qEy∝y,则得△Pa=△Pb>△Pc.故C错误.
D、动能增加量等于电场力做功,则得△Eka=△Ekb>△Ekc.故D错误.
故选:A
点评 本题一要掌握类平抛运动的研究方法;运动的分解法,二要能根据轨迹比较水平位移和竖直方向的关系,再选择比较对象,结合解析式进行比较.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.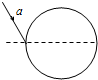 如图所示,是一种透明材料作成的圆柱形物体的横截面.一细束激光a沿着该横截面,以60°的入射角,从真空射入该圆柱形物体.已知这种材料的折射率为n=$\sqrt{3}$.假设激光是从透明圆柱体的最左端射入圆球的,则从该截面中能射出激光束的( )
如图所示,是一种透明材料作成的圆柱形物体的横截面.一细束激光a沿着该横截面,以60°的入射角,从真空射入该圆柱形物体.已知这种材料的折射率为n=$\sqrt{3}$.假设激光是从透明圆柱体的最左端射入圆球的,则从该截面中能射出激光束的( )
 如图所示,是一种透明材料作成的圆柱形物体的横截面.一细束激光a沿着该横截面,以60°的入射角,从真空射入该圆柱形物体.已知这种材料的折射率为n=$\sqrt{3}$.假设激光是从透明圆柱体的最左端射入圆球的,则从该截面中能射出激光束的( )
如图所示,是一种透明材料作成的圆柱形物体的横截面.一细束激光a沿着该横截面,以60°的入射角,从真空射入该圆柱形物体.已知这种材料的折射率为n=$\sqrt{3}$.假设激光是从透明圆柱体的最左端射入圆球的,则从该截面中能射出激光束的( )| A. | 只有1处 | B. | 只有2处 | C. | 只有3处 | D. | 可能有4处 |
1.如图1所示,某同学采用双线摆和光电计数器测定当地的重力加速度,已知每根悬线长为d,两悬点间相距s,金属小球半径为r,AB为光电计数器.现将小球垂直于纸面向外拉动,使悬线偏离竖直方向一个较小的角度并由静止释放,同时启动光电计数器,当小球第一次经过图中虚线(光束)位置O时,由A射向B的光束被挡住,计数器计数一次,显示为“1”,同时计时器开始计时,然后每当小球经过O点时,计数器都计数一次,当计数器上显示的计数次数刚好为n时,所用的时间为t,由此可知:

(1)双线摆的振动周期T=$\frac{2t}{n-1}$,双线摆的摆长L=$\sqrt{{d}^{2}-(\frac{s}{2})^{2}}$+r.
(2)该同学在实验中,测量5种不同摆长情况下单摆的振动周期,记录表格如下:
以L为横坐标,T2为纵坐标,在图2上作出T2-L图象,并利用此图象求得重力加速度g=9.86m/s2.(保留三位有效数字)

(1)双线摆的振动周期T=$\frac{2t}{n-1}$,双线摆的摆长L=$\sqrt{{d}^{2}-(\frac{s}{2})^{2}}$+r.
(2)该同学在实验中,测量5种不同摆长情况下单摆的振动周期,记录表格如下:
| L/m | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.41 | 1.79 | 1.90 | 2.00 | 2.19 |
| T2/s2 | 1.99 | 3.20 | 3.61 | 4.00 | 4.80 |
15.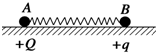 如图所示,真空中A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的均是弹性形变,则( )
如图所示,真空中A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的均是弹性形变,则( )
 如图所示,真空中A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的均是弹性形变,则( )
如图所示,真空中A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的均是弹性形变,则( )| A. | 保持Q不变,将q变为2q,平衡时弹簧的伸长量等于2x0 | |
| B. | 保持q不变,将Q变为2Q,平衡时弹簧的伸长量小于2x0 | |
| C. | 保持Q不变,将q变为-q,平衡时弹簧的缩短量等于x0 | |
| D. | 保持q不变,将Q变为-Q,平衡时弹簧的缩短量小于x0 |
 在验证机械能守恒的实验中,选出一条纸带如图所示,其中O点为起始点,A、B、C为三个计数点,打点计时器通以50Hz交流电,在计数点A和B之间,B和C之间还各有一个点,重锤的质量为m,根据以上数据,当打点针打到B点时重锤的重力势能比开始下落时减少了0.347J;这时它的动能是0.342J.g=9.8m/s2.
在验证机械能守恒的实验中,选出一条纸带如图所示,其中O点为起始点,A、B、C为三个计数点,打点计时器通以50Hz交流电,在计数点A和B之间,B和C之间还各有一个点,重锤的质量为m,根据以上数据,当打点针打到B点时重锤的重力势能比开始下落时减少了0.347J;这时它的动能是0.342J.g=9.8m/s2.
 如图所示,A、B、C三点都在匀强电场中,已知AC⊥BC,∠ABC=60°,BC=40cm.把一个电荷量q=10-5C的正电荷从A移到B,电场力做功为零;从B移到C,克服电场力做功3.46×10-3J.试求该匀强电场的电场强度(包括大小和方向).并画出经 A、B、C三点电场线.
如图所示,A、B、C三点都在匀强电场中,已知AC⊥BC,∠ABC=60°,BC=40cm.把一个电荷量q=10-5C的正电荷从A移到B,电场力做功为零;从B移到C,克服电场力做功3.46×10-3J.试求该匀强电场的电场强度(包括大小和方向).并画出经 A、B、C三点电场线.
