题目内容
18.如图所示,线圈工件加工车间的传送带不停地水平传送边长为L,质量为m,电阻为R的正方形线圈.在传送带的左端,线圈无初速地放在以恒定速度v匀速运动的传送带上,经过一段时间,达到与传送带相同的速度v,并通过一磁感应强度大小为B、方向竖直向上的匀强磁场,线圈与传送带始终保持相对静止.已知当一个线圈刚好开始匀速运动时,下一个线圈恰好放在传送带上;线圈匀速运动时,每两个线圈间保持距离L不变,匀强磁场的宽度为3L.求: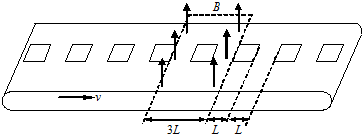
(1)每个线圈通过磁场区域产生的热量Q;
(2)在某个线圈加速的过程中,该线圈通过的距离s1和在这段时间里传送带通过的距离s2之比;
(3)传送带每传送一个线圈其电动机所消耗的电能E(不考虑电动机自身的能耗);
(4)当工件在传送带上持续传送的过程中,传送带传送工件的总功率P.
分析 (1)线圈匀速通过磁场,由Q=2Pt、P=$\frac{{E}^{2}}{R}$、E=BLv、t=$\frac{L}{v}$求解每个线圈通过磁场区域产生的热量Q.
(2)线圈做匀加速运动,传送带做匀速运动,由运动学位移公式求解离S1和S2之比.
(3)电动机多消耗的电能E转化为线圈的动能、摩擦产生的内能和焦耳热,根据能量守恒定律求解.
(4)先求出一个线圈加速度(即一个线圈进磁场和前一线圈出磁场的时间和)所用的时间,再根据P=$\frac{E}{t}$即可求解.
解答 解:(1)线圈感应电动势大小:E=BLv,
每个线圈通过磁场时间:t=$\frac{2L}{v}$,
每个线圈通过磁场产生热量:Q=$\frac{{E}^{2}}{R}$t,
解得:Q=$\frac{2{B}^{2}{L}^{3}v}{R}$;
(2)线圈做匀加速直线运动,位移:s1=$\frac{v}{2}$t,
传送带做匀速直线运动,位移:s2=vt,
位移之比:s1:s2=1:2;
(3)由(2)可知:s1:s2=1:2,则:s1:(s2-s1)=1:1,
线圈获得动能:EK=$\frac{1}{2}$mv2=fs1,
传送带上的热量损失:Q′=f(s2-s1)=$\frac{1}{2}$mv2,
电动机消耗的电能:E=EK+Q+Q′=mv2+$\frac{2{B}^{2}{L}^{3}v}{R}$;
(4)一个线圈加速所用的时间与一个线圈进磁场和前一线圈出磁场的时间和相等,为:t=$\frac{2L}{v}$,
传送带的功率:P=$\frac{E}{t}$=$\frac{{B}^{2}{L}^{2}{v}^{2}}{R}$+$\frac{m{v}^{3}}{2L}$;
答:(1)每个线圈通过磁场区域产生的热量Q为$\frac{2{B}^{2}{L}^{3}v}{R}$;
(2)在某个线圈加速的过程中,该线圈通过的距离s1和在这段时间里传送带通过的距离s2之比为1:2;
(3)传送带每传送一个线圈其电动机所消耗的电能E为mv2+$\frac{2{B}^{2}{L}^{3}v}{R}$;
(4)当工件在传送带上持续传送的过程中,传送带传送工件的总功率P为$\frac{{B}^{2}{L}^{2}{v}^{2}}{R}$+$\frac{m{v}^{3}}{2L}$.
点评 本题的解题关键是从能量的角度研究电磁感应现象,掌握焦耳定律、E=BLv、欧姆定律和能量如何转化是关键.

 如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长,圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h,圆环在C处获得一竖直向上的速度v,恰好能回到A,弹簧始终在弹性限度内,重力加速度为g,则圆环( )
如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长,圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h,圆环在C处获得一竖直向上的速度v,恰好能回到A,弹簧始终在弹性限度内,重力加速度为g,则圆环( )| A. | 下滑过程中,加速度一直减小 | |
| B. | 下滑过程中,克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| C. | 在C处,弹簧的弹性势能为$\frac{1}{4}$mv2-mgh | |
| D. | 上滑经过B的速度大于下滑经过B的速度 |
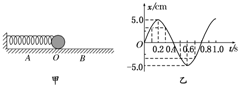 如图甲所示为以O点为平衡位置,在A、B两点间做简谐运动的弹簧振子,图乙为这个弹簧振子的振动图象,由图可知下列说法中正确的是( )
如图甲所示为以O点为平衡位置,在A、B两点间做简谐运动的弹簧振子,图乙为这个弹簧振子的振动图象,由图可知下列说法中正确的是( )| A. | 在t=0.2s时,弹簧振子的加速度为正向最大 | |
| B. | 在t=0.1s与t=0.3s两个时刻,弹簧振子在同一位置 | |
| C. | 从t=0到t=0.2s时间内,弹簧振子做加速度增加的减速运动 | |
| D. | 在t=0.6s时,弹簧振子有最小的弹性势能 |
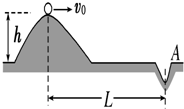 随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴.则( )
随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴.则( )| A. | 球被击出后做平抛运动 | |
| B. | 该球从被击出到落入A穴所用的时间为$\sqrt{\frac{h}{g}}$ | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{2g}{h}}$ | |
| D. | 球被击出后受到的水平风力的大小为$\frac{mgh}{L}$ |
 如图所示,在光滑水平面的左侧固定一竖直挡板,A球在水平面上静止放置,B球向左运动与A球发生正碰,B球碰撞前、后的速率之比为3:1,A球垂直撞向挡板,碰后原速率返回,两球刚好不发生第二次碰撞,A、B两球的质量之比为4:1,A、B碰撞前、后两球总动能之比为9:5.
如图所示,在光滑水平面的左侧固定一竖直挡板,A球在水平面上静止放置,B球向左运动与A球发生正碰,B球碰撞前、后的速率之比为3:1,A球垂直撞向挡板,碰后原速率返回,两球刚好不发生第二次碰撞,A、B两球的质量之比为4:1,A、B碰撞前、后两球总动能之比为9:5.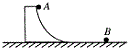 如图所示,质量为2m、高度为h的光滑弧形槽末端水平,放置在光滑水平地面上,质量为m的小球A从弧形槽顶端静止释放,之后与静止在水平面上质量为m的小球B发生对心碰撞并粘在一起.求:
如图所示,质量为2m、高度为h的光滑弧形槽末端水平,放置在光滑水平地面上,质量为m的小球A从弧形槽顶端静止释放,之后与静止在水平面上质量为m的小球B发生对心碰撞并粘在一起.求: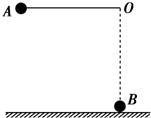 如图所示,一质量为2m的小球A用长为L=0.5m的轻绳与悬点O相连,O点离地面的高为L,在O点正下方的光滑地面上放置一质量为m的小球B,将A球放置在与O点等高的位置,且将绳拉直,A、B、O在同一个竖直平面内,现将小球A由静止释放,求A、B球碰撞后,B球可能获得的最大速度.
如图所示,一质量为2m的小球A用长为L=0.5m的轻绳与悬点O相连,O点离地面的高为L,在O点正下方的光滑地面上放置一质量为m的小球B,将A球放置在与O点等高的位置,且将绳拉直,A、B、O在同一个竖直平面内,现将小球A由静止释放,求A、B球碰撞后,B球可能获得的最大速度.
