题目内容
3.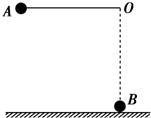 如图所示,一质量为2m的小球A用长为L=0.5m的轻绳与悬点O相连,O点离地面的高为L,在O点正下方的光滑地面上放置一质量为m的小球B,将A球放置在与O点等高的位置,且将绳拉直,A、B、O在同一个竖直平面内,现将小球A由静止释放,求A、B球碰撞后,B球可能获得的最大速度.
如图所示,一质量为2m的小球A用长为L=0.5m的轻绳与悬点O相连,O点离地面的高为L,在O点正下方的光滑地面上放置一质量为m的小球B,将A球放置在与O点等高的位置,且将绳拉直,A、B、O在同一个竖直平面内,现将小球A由静止释放,求A、B球碰撞后,B球可能获得的最大速度.
分析 由机械能守恒定律求出A球到达底端时的速度,两球碰撞过程动量守恒,应用动量守恒定律与能量守恒定律可以求出B的速度.
解答 解:A球下落过程中,由机械能守恒有:
2mgL=$\frac{1}{2}$×2mv02,
当两球发生弹性碰撞后,B球获得的速度最大,
以向右为正方向,由动量守恒定律得:
2mv0=2mv1+mv2,
$\frac{1}{2}$×2mv02=$\frac{1}{2}$×2mv12+$\frac{1}{2}$mv22,
解得:v2=$\frac{4}{3}$$\sqrt{2gL}$;
答:B球可能获得的最大速度为$\frac{4}{3}$$\sqrt{2gL}$.
点评 本题考查了求球的最大速度,分析清楚运动过程,应用机械能守恒定律、动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
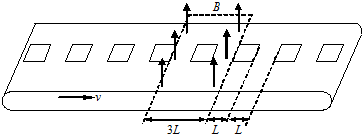
11. 如图为某探究活动小组设计的节能运输系统的简化示意图.斜面轨道倾角为37°,质量为M的货箱与轨道的动摩擦因数为0.5.货箱在轨道顶端时,自动装货装置将质量为m的货物装入货箱,然后货箱载着货物沿轨道无初速滑下,当轻弹簧压缩至最短时,自动卸货装置立刻将货物卸下,然后货箱恰好被弹回到轨道顶端,再重复上述过程.已知sin37°=0.6,cos37°=0.8,下列选项正确的是( )
如图为某探究活动小组设计的节能运输系统的简化示意图.斜面轨道倾角为37°,质量为M的货箱与轨道的动摩擦因数为0.5.货箱在轨道顶端时,自动装货装置将质量为m的货物装入货箱,然后货箱载着货物沿轨道无初速滑下,当轻弹簧压缩至最短时,自动卸货装置立刻将货物卸下,然后货箱恰好被弹回到轨道顶端,再重复上述过程.已知sin37°=0.6,cos37°=0.8,下列选项正确的是( )
 如图为某探究活动小组设计的节能运输系统的简化示意图.斜面轨道倾角为37°,质量为M的货箱与轨道的动摩擦因数为0.5.货箱在轨道顶端时,自动装货装置将质量为m的货物装入货箱,然后货箱载着货物沿轨道无初速滑下,当轻弹簧压缩至最短时,自动卸货装置立刻将货物卸下,然后货箱恰好被弹回到轨道顶端,再重复上述过程.已知sin37°=0.6,cos37°=0.8,下列选项正确的是( )
如图为某探究活动小组设计的节能运输系统的简化示意图.斜面轨道倾角为37°,质量为M的货箱与轨道的动摩擦因数为0.5.货箱在轨道顶端时,自动装货装置将质量为m的货物装入货箱,然后货箱载着货物沿轨道无初速滑下,当轻弹簧压缩至最短时,自动卸货装置立刻将货物卸下,然后货箱恰好被弹回到轨道顶端,再重复上述过程.已知sin37°=0.6,cos37°=0.8,下列选项正确的是( )| A. | 货箱载着货物接触弹簧时立即开始减速运动 | |
| B. | 货物质量m应为货箱质量M的4倍 | |
| C. | 货箱不与弹簧接触时,上滑的加速度大于下滑的加速度 | |
| D. | 货箱从最低点滑回顶端的过程中,弹簧的弹性势能全部转化为货箱的重力势能 |
8.电磁灶是利用电磁感应原理加热的一种新型灶具,下列对电磁灶的相关说法中正确的是( )
| A. | 加热用锅体其材料可采用陶瓷 | |
| B. | 锅体中的涡流是由恒定的磁场产生的 | |
| C. | 锅体中的涡流是由变化的磁场产生的 | |
| D. | 提高磁场变化的频率,可提高电磁灶的加热效果 |
15. 远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R.变压器为理想变压器,则下列关系式中正确的是( )
远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R.变压器为理想变压器,则下列关系式中正确的是( )
 远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R.变压器为理想变压器,则下列关系式中正确的是( )
远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R.变压器为理想变压器,则下列关系式中正确的是( )| A. | $\frac{{I}_{1}}{{I}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$ | B. | I2=$\frac{{U}_{2}}{R}$ | C. | I1U1>I22R | D. | I1U1=I2U2 |
12. 被拉直的绳子一端固定在天花板上,另一端系着小球.小球从A点静止释放,运动到B点的过程中,不计空气阻力.则( )
被拉直的绳子一端固定在天花板上,另一端系着小球.小球从A点静止释放,运动到B点的过程中,不计空气阻力.则( )
 被拉直的绳子一端固定在天花板上,另一端系着小球.小球从A点静止释放,运动到B点的过程中,不计空气阻力.则( )
被拉直的绳子一端固定在天花板上,另一端系着小球.小球从A点静止释放,运动到B点的过程中,不计空气阻力.则( )| A. | 小球受到的拉力先变小后变大 | B. | 小球的机械能守恒 | ||
| C. | 小球的切向加速度一直变大 | D. | 小球的动能先变大后变小 |
13.建立物理模型是物理研究的常用方法,下列属于理想化“物理模型”的是( )
| A. | 重力 | B. | 向心力 | C. | 元电荷 | D. | 点电荷 |
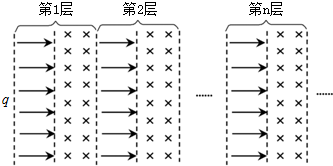
 一台质谱仪的工作原理如图所示,电荷量均为+q、质量不同的离子飘入电压为U0的加速电场,其初速度几乎为零,这些离子经加速后通过狭缝O沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场,最后打在底片上,已知放置底片的区域MN=L,且OM=L.某次测量发现MN中左侧$\frac{2}{3}$区域MQ损坏,检测不到离子,但右侧$\frac{1}{3}$区域QN仍能正常检测到离子,在适当调节加速电压后,原本打在MQ的离子即可在QN检测到.
一台质谱仪的工作原理如图所示,电荷量均为+q、质量不同的离子飘入电压为U0的加速电场,其初速度几乎为零,这些离子经加速后通过狭缝O沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场,最后打在底片上,已知放置底片的区域MN=L,且OM=L.某次测量发现MN中左侧$\frac{2}{3}$区域MQ损坏,检测不到离子,但右侧$\frac{1}{3}$区域QN仍能正常检测到离子,在适当调节加速电压后,原本打在MQ的离子即可在QN检测到.