题目内容
【题目】如图所示，在磁感应强度为2T、方向垂直纸面向里的匀强磁场中，金属杆MN在平行金属导轨上以速度1m/s向右匀速滑动，两导轨间距为0.5m，金属杆MN的电阻为1Ω，外电路连接的电阻R为4Ω，其他电阻不计，则通过R的电流方向和R两端的电压分别是（ ）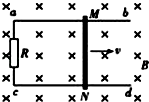
A.a→c，0.8V
B.c→a，0.8V
C.c→a，1V
D.a→c，1V
【答案】A
【解析】解：由右手定则判断可知，MN中产生的感应电流方向为N→M，则通过电阻R的电流方向为a→c．
MN产生的感应电动势公式为E=BLv=2×0.5×1=1V；
R两端的电压为：U= 
= 
=0.8V．
故A正确，BCD错误．
故选：A．
【考点精析】通过灵活运用楞次定律，掌握楞次定律适用于一般情况的感应电流方向的判定，而右手定则只适用于导线切割磁感线运动的情况，此种情况用右手定则判定比用楞次定律判定简便即可以解答此题．
练习册系列答案
ABC考王全优卷系列答案
相关题目
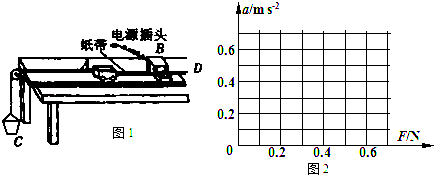
【题目】为了“探究加速度与力、质量的关系”，现提供如图1所示的器材：A为小车，B为电火花计时器，C为装有沙子的小桶，D为一端带有定滑轮的长方形木板．保持小车的质量不变，改变小桶中沙子的质量（实验中认为细绳对小车拉力F等于沙子和小桶的总重力），测得小车所受绳子的拉力F和加速度a的数据如表：
F/N | 0.21 | 0.30 | 0.40 | 0.49 | 0.60 |
a/（ms﹣2） | 0.10 | 0.21 | 0.29 | 0.41 | 0.49 |
①根据测得的数据，在图2中作出a﹣F图象；
②对你作出的图象进行分析，可得出小车与长木板之间的摩擦力Ff=N．
