Question

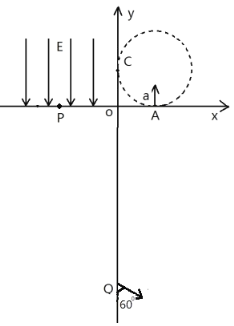
【题目】如图所示，在xOy竖直平面内，长L的绝缘轻绳一端固定在第一象限的P点，另一端栓有一质量为m、带电荷量为+q的小球，OP距离也为L且与x轴的夹角为60°，在x轴上方有水平向左的匀强电场,场强大小为mg，在x轴下方有竖直向上的匀强电场，场强大小为，过O和P两点的虚线右侧存在方向垂直xOy平面向外、磁感应强度为B的匀强磁场。小球置于y轴上的C点时，绳恰好伸直且与y轴夹角为30°，小球由静止释放后将沿CD方向做直线运动，到达D点时绳恰好绷紧，小球沿绳方向的分速度立即变为零，并以垂直于绳方向的分速度摆下，到达O点时将绳断开。不计空气阻力。求：

(1)小球刚释放瞬间的加速度大小a；

(2)小球到达O点时的速度大小v；

(3)小球从O点开始到第二次到达x轴（不含O点）所用的时间t.

Answer 1

【答案】（1）；（2）；（3）+

【解析】

（1）如图所示，小球由静止释放时，所受重力和电场力的合力大小为：F=

根据牛顿第二定律有：F合=ma，

解得：

（2）设小球到达D点时的速度为v0，由运动学公式有：v02=2aL，

垂直于绳方向的分速度为：v1=v0cos30，

解得：v1=

从D点到O点的过程中，由动能定理得：mgLcos30-qE1L(1-sin30)=mv2-mv12

解得：v=

（3）因为qE2=mg,小球从O点以v垂直于虚线进入磁场将做匀速圆周运动,

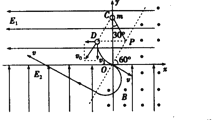
根据牛顿第二定律有：qvB=m

得半径为：

周期为：

小球进入磁场中运动圆周后又垂直于虚线射出磁场，以v做匀速直线运动第一次打在x轴上，匀速直线运动的距离为d=2rtan60=2r，

t1= ；

小球再次进入电场E1后，小球所受重力和电场力的合力垂直于v，小球做类平抛运动，

解得

所以t=t1+t2+t3 =