题目内容
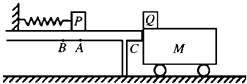
【题目】如图所示,质量为![]() =2kg的长方体形木板B静止在足够大的水平地面上,质量为
=2kg的长方体形木板B静止在足够大的水平地面上,质量为![]() =lkg的木箱A静止在木板B上,一根细直的轻绳一端拴在木箱上,另一端拴在地面的木桩上,与水平面的夹角为θ=37°,己知木箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4,各接触面之间最大静摩擦力等于其滑动摩擦力。现用水平恒力F将木板B从木箱A下面以a=6m/s的加速度匀加速抽出。(sin37°=0.6,cos37°=0.8,g取10m/s)试求:
=lkg的木箱A静止在木板B上,一根细直的轻绳一端拴在木箱上,另一端拴在地面的木桩上,与水平面的夹角为θ=37°,己知木箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4,各接触面之间最大静摩擦力等于其滑动摩擦力。现用水平恒力F将木板B从木箱A下面以a=6m/s的加速度匀加速抽出。(sin37°=0.6,cos37°=0.8,g取10m/s)试求:

(1)求此过程中轻绳上张力所的大小;
(2)求此过程中水平恒力F的大小;
(3)若没有此轻绳,仍然要将木板B从木箱A下抽出,求水平恒力F的最小值。
【答案】(1)![]() =10N ;(2)F=32.4N (3)F=27N
=10N ;(2)F=32.4N (3)F=27N
【解析】⑴隔离木箱A,对A进行受力分析,如图甲所示:
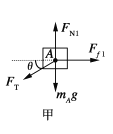
由平衡条件得:
![]()
![]()
![]()
代入数据得: ![]() ,
, ![]() ;
;
⑵对B进行受力分析,如图乙所示.
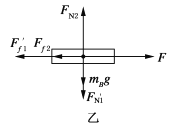
由牛顿第二定律得: ![]()
![]()
![]()
![]()
解得: ![]()
⑶对A根据牛顿第二定律: ![]()
对B根据牛顿第二定律: ![]()
B从A下抽出的条件: ![]()
![]()
解得: ![]() ,即最小值为:
,即最小值为: ![]() 。
。

练习册系列答案
相关题目