��Ŀ����
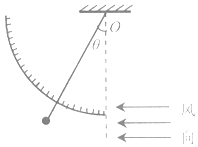
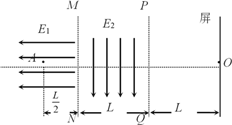
����Ŀ����ͼ��ʾ������MN�����һ���糡ǿ��E1=E����ǿ�糡��������ƽ�е�ֱ��MN��PQ֮������ſ�ΪL���糡ǿ��ΪE2=2E����ǿ�糡��������PQ�Ҳ����ΪL����һ��糡E2ƽ�е������ֽ�һ���ӣ������e������Ϊm���������������ٶȷ���糡E1�е�A�㣬A�㵽MN�ľ���Ϊ![]() �������Ӵ����Ҳ��������AO����������ֱ������ΪO����
�������Ӵ����Ҳ��������AO����������ֱ������ΪO����
(1)���Ӵ��ͷŵ����������õ�ʱ��t��
(2)���Ӹ�����糡E2ʱ���ٶȷ�����AO���нǵ�����ֵtan����
(3)���Ӵ����ϵĵ�P����O��ľ���x��
���𰸡���1��![]() ��2��2��3��3L
��2��2��3��3L
��������(1)�����ڵ糡E1�������ٶ�Ϊ����ȼ���ֱ���˶�������ٶ�Ϊa1��ʱ��Ϊt1����ţ�ٵڶ����ɵã� ![]()
��![]() �ã�
�ã� ![]()
���ӽ���糡E2ʱ���ٶ�Ϊ��v1=a1t1
����糡E2����ˮƽ����������ֱ���˶���ʱ��Ϊ�� ![]()
���糡������ʱ��Ϊ�� ![]()
���Ӵ��ͷŵ����������õ�ʱ��Ϊ��t=t1+t2+t3
�������ã� ![]()
(2)����������糡E2ʱƽ�е糡������ٶ�Ϊvy����ţ�ٵڶ����ɵã����ӽ���糡E2ʱ�ļ��ٶ�Ϊ�� ![]()
vy=a2t3
![]()
���Ӹ�����糡E2ʱ���ٶȷ�����AO���нǵ�����ֵΪ![]()
�����ã�tan��=2
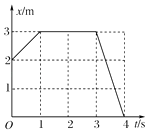
(3)���������ڵ糡�е��˶��켣��ͼ��ʾ:
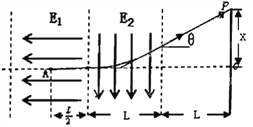
����Ӵ����ϵĵ�P��O��ľ���x��������ͼ�м��ι�ϵ�ã� 
�����ã�x=3L��

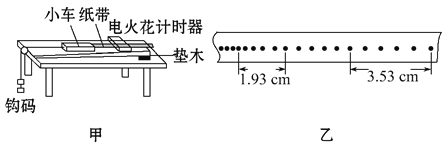
����Ŀ��ijͬѧ����̽�������͵����쳤�Ĺ�ϵ��ʵ���У��������ͼ1��ʾ��ʵ��װ�ã����õĹ���ÿֻ����������30g�����Ȳ�����ҹ���ʱ���ɵ���Ȼ���ȣ��ٽ�5������������ڵ��ɵ��¶ˣ�ÿ�ζ������Ӧ�ĵ����ܳ��ȣ�����������������ı��У�������ʼ��δ���������ȣ�ȡg=9.8m/s2��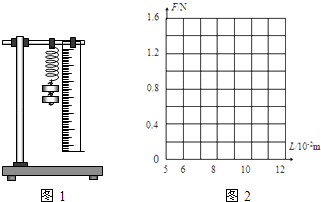
����������g�� | 0 | 30 | 60 | 90 | 120 | 150 |
�����ܳ���cm�� | 5.00 | 6.16 | 7.34 | 8.48 | 9.64 | 10.81 |
��1���Ը�����Щʵ��������ͼ2����������ֽ�������������ܵ�����СF�������ܳ�L֮��ĺ�����ϵͼ�ߣ�
��2���õ��ɵľ���k��N/m