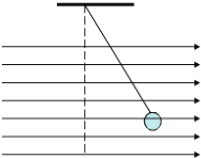
题目内容
【题目】宇宙中某一质量为
、半径为
的星球，有三颗卫星A、B、C在同一平面上沿逆时针方向做圆周运动，其位置关系如图所示。其中A到该星球表面的高度为
，已知万有引力常量为
，则下列说法正确的是
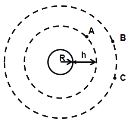
A. 卫星A的公转周期为
B. 卫星C加速后可以追到卫星B
C. 三颗卫星的线速度大小关系为
D. 三颗卫星的向心加速度大小关系为
【答案】C
【解析】
卫星绕地球做圆周运动，万有引力提供圆周运动向心力，并由此分析向心加速度等描述圆周运动的物理量与半径的关系并由此展开分析即可.
A、根据万有引力提供圆周运动向心力，可得周期
，A卫星的轨道半径为
，则
；故A错误.
B、卫星在轨道上加速或减速将改变圆周运动所需向心力，而提供向心力的万有引力保持不变，故卫星在轨道上加速或减速时卫星将做离心运动或近心运动而改变轨道高度，故不能追上或等候同一轨道上的卫星；需要C卫星先减速后加速才能追上B卫星；故B错误.
C、根据万有引力提供圆周运动向心力可得线速度
，知半径越大线速度越小，因
，可知
；故C正确.
D、根据万有引力提供圆周运动向心力可得加速度
，知半径越大加速度越小，因，可知
；故D错误.
故选C.
练习册系列答案
阅读快车系列答案
相关题目
