题目内容
质量为m=4Kg的物体与水平面间的动摩擦因数μ=0.2,今用F=16N的水平恒力使该物体由静止开始在水平面内做匀加速直线运动(g取10m/s2).求:(1)物体运动的加速度;(2)前4s内力F对物体所做的功.
【答案】分析:物体竖直方向受到重力和水平面的支持力,两力平衡.水平方向受到水平恒力F和滑动摩擦力,产生加速度,根据牛顿第二定律求解加速度.由位移公式求出前4s内物体的位移x,再公式W=Fx求出F对物体做的功.
解答:解:
(1)设物体的加速度为a,根据牛顿第二定律得
F-μmg=ma
得到 a=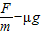 =
=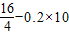 (m/s2)=2m/s2
(m/s2)=2m/s2
(2)前4s内物体的位移为x=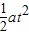 =
=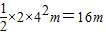
前4s内F对物体所做的功W=Fx=16×16J=256J.
答:(1)物体运动的加速度是2m/s2;(2)前4s内力F对物体所做的功是256J.
点评:本题是求功的问题,由功的计算公式W=Flcosα可知,关键确定三个要素:力的大小F,位移的大小l和力与位移的夹角α.
解答:解:
(1)设物体的加速度为a,根据牛顿第二定律得
F-μmg=ma
得到 a=
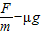 =
=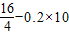 (m/s2)=2m/s2
(m/s2)=2m/s2(2)前4s内物体的位移为x=
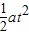 =
=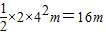
前4s内F对物体所做的功W=Fx=16×16J=256J.
答:(1)物体运动的加速度是2m/s2;(2)前4s内力F对物体所做的功是256J.
点评:本题是求功的问题,由功的计算公式W=Flcosα可知,关键确定三个要素:力的大小F,位移的大小l和力与位移的夹角α.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
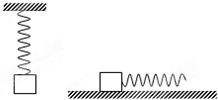 原长l0=12cm的弹簧,上端固定,下端挂质量为m=4kg的物块,静止时弹簧长度l1=20cm.当将该物块放在水平桌面上,并用上述弹簧沿水平方向拉物块.当弹簧长度为l2=15cm时,物块恰好被拉动.此后为保持物块做匀速直线运动,弹簧长度维持在l3=14cm..求:
原长l0=12cm的弹簧,上端固定,下端挂质量为m=4kg的物块,静止时弹簧长度l1=20cm.当将该物块放在水平桌面上,并用上述弹簧沿水平方向拉物块.当弹簧长度为l2=15cm时,物块恰好被拉动.此后为保持物块做匀速直线运动,弹簧长度维持在l3=14cm..求: 质量为M=4kg的长木板,上表面粗糙,下表面光滑,静止地放在光滑的水平地面上.在长木板的左、右两端各放着一个小物块A和B,如图所示.已知mA=2kg、mB=1kg,两物块与长木板之间的动摩擦因数都是0.2.现同时用力分别击打A、B,使它们在瞬间同时获得方向相反、大小都是v0=7m/s的水平速度,此后它们在木板上相向滑行,并且在滑行过程中它们始终没有相碰,取g=10m/s2.问:
质量为M=4kg的长木板,上表面粗糙,下表面光滑,静止地放在光滑的水平地面上.在长木板的左、右两端各放着一个小物块A和B,如图所示.已知mA=2kg、mB=1kg,两物块与长木板之间的动摩擦因数都是0.2.现同时用力分别击打A、B,使它们在瞬间同时获得方向相反、大小都是v0=7m/s的水平速度,此后它们在木板上相向滑行,并且在滑行过程中它们始终没有相碰,取g=10m/s2.问: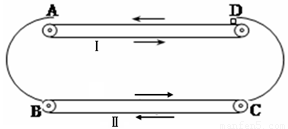
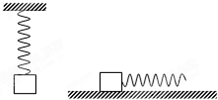 原长l0=12cm的弹簧,上端固定,下端挂质量为m=4kg的物块,静止时弹簧长度l1=20cm.当将该物块放在水平桌面上,并用上述弹簧沿水平方向拉物块.当弹簧长度为l2=15cm时,物块恰好被拉动.此后为保持物块做匀速直线运动,弹簧长度维持在l3=14cm..求:
原长l0=12cm的弹簧,上端固定,下端挂质量为m=4kg的物块,静止时弹簧长度l1=20cm.当将该物块放在水平桌面上,并用上述弹簧沿水平方向拉物块.当弹簧长度为l2=15cm时,物块恰好被拉动.此后为保持物块做匀速直线运动,弹簧长度维持在l3=14cm..求: