��Ŀ����
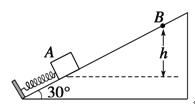
����Ŀ����ͼ��ʾΪһ�����εĿӣ����пӱ�Ե����M��N��Բ�ĵȸ�����ͬһ��ֱ���ڡ��ּס�����λͬѧ�ֱ�վ��M��N���㣬ͬʱ������С����v1��v2���ٶ���ͼʾ����ˮƽ�׳�����������պ����ڿ���ͬһ��Q����֪��MOQ��60�������Կ���������������˵����ȷ����

A. ����������֮��Ϊ1��3
B. ��������v1�����������������֮ǰ��ײ
C. ����ij��ٶ����������仯��ֻҪ���ڿ��е�ͬһ�㣬�����׳�������֮�Ͳ���
D. ������M��ˮƽ�׳�С�ı�С���׳����ٶȣ�С����ܴ�ֱ�ӱ��������
���𰸡�AB
�����������ݼ��ι�ϵ֪��Q��O���ˮƽ����ľ������0.5R������M��ˮƽλ��![]() ��N��ˮƽλ��Ϊ��
��N��ˮƽλ��Ϊ�� ![]() ��������Q���ˮƽλ��֮��Ϊ1:3���˶�ʱ����ȣ�����ٶ�֮��Ϊ1��3����A��ȷ����ֻ����v1����v2���䣬��M�˶��Ĺ켣����㽫����һЩ��������ڿ�����������B��ȷ��Ҫ��С�����ڻ����ϵ�ͬһ��,��ˮƽλ��֮��Ϊ2R����(v1+v2)t=2R����㲻ͬ����ֱ����λ�ƾͲ�ͬ��tҲ��ͬ������v1+v2Ҳ����һ����ֵ����C������ƽ���˶������ۣ��ٶȵķ����ӳ��߽�ˮƽλ�Ƶ��е㣬��Ϊ����O������ˮƽλ�Ƶ��е㣬���Բ�����ʹС���ذ뾶��������Բ������ڣ���D��������AB��ȷ��CD����
��������Q���ˮƽλ��֮��Ϊ1:3���˶�ʱ����ȣ�����ٶ�֮��Ϊ1��3����A��ȷ����ֻ����v1����v2���䣬��M�˶��Ĺ켣����㽫����һЩ��������ڿ�����������B��ȷ��Ҫ��С�����ڻ����ϵ�ͬһ��,��ˮƽλ��֮��Ϊ2R����(v1+v2)t=2R����㲻ͬ����ֱ����λ�ƾͲ�ͬ��tҲ��ͬ������v1+v2Ҳ����һ����ֵ����C������ƽ���˶������ۣ��ٶȵķ����ӳ��߽�ˮƽλ�Ƶ��е㣬��Ϊ����O������ˮƽλ�Ƶ��е㣬���Բ�����ʹС���ذ뾶��������Բ������ڣ���D��������AB��ȷ��CD����