题目内容
【题目】如图所示,将一轻弹簧固定在倾角为30°的斜面底端,现用一质量为m的物体将弹簧压缩锁定在A点,解除锁定后,物体将沿斜面上滑,物体在运动过程中所能到达的最高点B距A点的竖直高度为h,物体离开弹簧后沿斜面向上运动的加速度大小等于重力加速度g.则下列说法正确的是 ( )
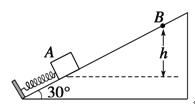
A. 弹簧的最大弹性势能为mgh
B. 物体从A点运动到B点的过程中系统损失的机械能为mgh
C. 物体的最大动能等于弹簧的最大弹性势能
D. 物体最终静止在B点
【答案】BD
【解析】试题分析:根据能量守恒,在物块上升到最高点的过程中,弹性势能变为物块的重力势能mgh和内能,故弹簧的最大弹性势能应大于mgh,故A错误;物体离开弹簧后沿斜面向上运动的加速度大小等于重力加速度g,由牛顿第二定律得物块所受沿斜面向下的合力为,F=mg,而重力沿斜面向下的分量为mgsin30°=![]() mg,
mg,
可知,物块必定受到沿斜面向下的摩擦力为f=![]() mg,摩擦力做功等于物体从A点运动到B点的过程中系统损失的机械能,
mg,摩擦力做功等于物体从A点运动到B点的过程中系统损失的机械能,![]() ,故B正确;物体动能最大时,加速度为零,此时物块必定沿斜面向上移动了一定距离,故损失了一部分机械能,所以动能小于弹簧的最大弹性势能,故C错误;由于物体到达B点后,瞬时速度为零,此后摩擦力方向沿斜面向上,与重力沿斜面向下的分力相抵消,物块将静止在B点,故D正确.故选BD。
,故B正确;物体动能最大时,加速度为零,此时物块必定沿斜面向上移动了一定距离,故损失了一部分机械能,所以动能小于弹簧的最大弹性势能,故C错误;由于物体到达B点后,瞬时速度为零,此后摩擦力方向沿斜面向上,与重力沿斜面向下的分力相抵消,物块将静止在B点,故D正确.故选BD。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目