题目内容
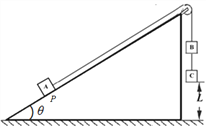
【题目】如图所示,有A、B、C三个物块,一根轻绳绕过光滑的轻质定滑轮,两端分别连接物块A与物块B,物块B的下面通过轻绳与物块C连接,物体B和C的质量均为m,物块A的质量为3m,物块A锁定在光滑的斜面上的P点(P点离滑轮足够远),斜面倾角为θ=300,轻绳始终平行于斜面。物块B与物块C之间的轻绳长度为L,初始时C离地的高度也为L。解除对物体A的锁定,物块开始运动.设物块A可视为质点,物块B与物块C落地后不反弹,重力加速度大小为g. 求:
(1)A刚上升时的加速度;
(2)A上升过程的最大速度;
(3)A能上升的最高位置离P点的距离。
【答案】(1)g/5;(2)![]() ;(3)
;(3)![]() ;
;
【解析】(1)解除对A的锁定后,A加速上升,B和C加速下降,加速度a大小相等,设轻绳对A和B的拉力大小为T,由牛顿第二定律得
对A:T-3mgsinθ=3ma
对B、C:(m+m)g-T’=(m+m)a
联立解得![]()
(2)当物块C刚着地时,A的速度最大.从A刚开始上升到C刚着地的过程,
由机械能守恒定律得: ![]()
解得![]()
(3)设C落地后A沿斜面继续上升d时速度为零,此时B下降d未接触地面,A和B组成的系统满足械能守恒定律得: ![]()
联立解得![]()
由于![]() ,B不会触地,
,B不会触地,
所以A能上升的最高位置离P点的距离![]()

练习册系列答案
相关题目