题目内容
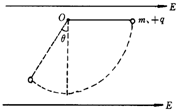
如图所示,在方向水平向右的匀强电场中,一不可伸长的绝缘细线的一端连着一个带电量为q、质量为m的带正电的小球,另一端固定于O点.把小球拉起至细线与场强平行,然后无初速释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ,θ=37°.求:
(1)电场强度E的大小;
(2)小球经过最低点时绳子的拉力大小;
(3)小球经过最低点时小球的加速度.
(1)电场强度E的大小;
(2)小球经过最低点时绳子的拉力大小;
(3)小球经过最低点时小球的加速度.

(1)对全过程运用动能定理得,mglcosθ-Eql(1+sinθ)=0
解得E=
(2)对小球从释放到最低点运用动能定理得,mgl-Eql=
mv2
解得v=
根据牛顿第二定律得,T-mg=m
解得T=2mg
(3)向心加速度a1=
=g
切向加速度a2=
=
g
根据平行四边形定则知,a=
=
g.
答:(1)电场强度E的大小为
;
(2)小球经过最低点时绳子的拉力大小为2mg;
(3)小球经过最低点时小球的加速度为
g.
解得E=
| mg |
| 2q |
(2)对小球从释放到最低点运用动能定理得,mgl-Eql=
| 1 |
| 2 |
解得v=
| gl |
根据牛顿第二定律得,T-mg=m
| v2 |
| l |
解得T=2mg
(3)向心加速度a1=
| v2 |
| l |
切向加速度a2=
| qE |
| m |
| 1 |
| 2 |
根据平行四边形定则知,a=
| a12+a22 |
| ||
| 2 |
答:(1)电场强度E的大小为
| mg |
| 2q |
(2)小球经过最低点时绳子的拉力大小为2mg;
(3)小球经过最低点时小球的加速度为
| ||
| 2 |

练习册系列答案
相关题目