题目内容
3. 如图所示,质量为m的小球被固定在轻杆的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力的作用.设某一时刻小球通过轨道的最低点,此时轻杆对小球的拉力为7.5mg,此后小球继续做圆周运动,经过半个圆周通过最高点时轻杆对小球的支持力为0.5mg,小球在此半个圆周运动过程中克服空气阻力所做的功为( )
如图所示,质量为m的小球被固定在轻杆的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力的作用.设某一时刻小球通过轨道的最低点,此时轻杆对小球的拉力为7.5mg,此后小球继续做圆周运动,经过半个圆周通过最高点时轻杆对小球的支持力为0.5mg,小球在此半个圆周运动过程中克服空气阻力所做的功为( )| A. | $\frac{mgR}{4}$ | B. | $\frac{mgR}{2}$ | C. | mgR | D. | 2mgR |
分析 圆周运动在最高点和最低点沿径向的合力提供向心力,根据牛顿第二定律求出最高点和最低点的速度,再根据动能定理求出此过程中小球克服空气阻力所做的功.
解答 解:小球在最低点时,由牛顿第二定律得:
7.5mg-mg=m$\frac{{v}_{1}^{2}}{R}$
小球在最高点时,有:mg-0.5mg=m$\frac{{v}_{2}^{2}}{R}$
小球由最低点到最高点的过程中,由动能定理得:-2mgR-Wf=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12
解得 Wf=mgR.
故选:C
点评 运用动能定理解题要确定好研究的过程,找出有多少力做功,然后列动能定理表达式求解.

练习册系列答案
相关题目
14.线圈在匀强磁场中匀速转动,产生的交变电流如图,则( )


| A. | 在A和C时刻线圈平面和磁场平行 | |
| B. | 在A和C时刻线圈平面和磁场垂直 | |
| C. | 在B时刻线圈中的磁通量为零 | |
| D. | 若线圈转动的周期为0.02,则该交变电流的频率为50Hz |
15.下列关于电场强度和电势的说法中,正确的是( )
| A. | 电场强度为零的地方,电势一定为零 | |
| B. | 电势为零的地方,电场强度一定为零 | |
| C. | 电场强度较大的地方,电场线一定较密 | |
| D. | 沿着电场强度的方向,电势逐渐降低 |
12.有两个共点力,它们的合力大小为7N,其中一个力的大小为10N,则另一个力的大小不可能为( )
| A. | 12N | B. | 2N | C. | 8N | D. | 14N |
 如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C,方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:m0=6.64×10-27kg,q0=3.2×10-19C,初速率v=3.2×106m/s.(sin37°=0.6,cos37°=0.8)求:
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C,方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:m0=6.64×10-27kg,q0=3.2×10-19C,初速率v=3.2×106m/s.(sin37°=0.6,cos37°=0.8)求: 如图所示,一水平传送带两轮间距为20m,以2m/s的速度做匀速运动.已知某物体与传送带间的动摩擦因数为0.1,现将该物体由静止轻放到传送带的A端.求:
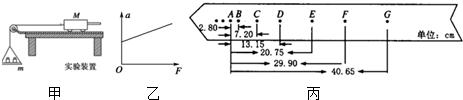
如图所示,一水平传送带两轮间距为20m,以2m/s的速度做匀速运动.已知某物体与传送带间的动摩擦因数为0.1,现将该物体由静止轻放到传送带的A端.求: 在“用打点计时器测速度”的实验中,小车拖着纸带运动,打出的纸带如图所示.选出A、B、C、D、E共5个计数点,每相邻两点间还有四个计时点(图中未画出),以A点为起点量出的到各点的位移已标在图上.由此可求得打下B点时小车运动的速度约为vB=0.17m/s;打下D点时小车运动的速度约为vD=0.21m/s.(结果保留二位有效数字)
在“用打点计时器测速度”的实验中,小车拖着纸带运动,打出的纸带如图所示.选出A、B、C、D、E共5个计数点,每相邻两点间还有四个计时点(图中未画出),以A点为起点量出的到各点的位移已标在图上.由此可求得打下B点时小车运动的速度约为vB=0.17m/s;打下D点时小车运动的速度约为vD=0.21m/s.(结果保留二位有效数字) 若用如图所示的电路完成 实验,如果两电表的读数分别为U和I,测得拉直后电阻丝的长度为L、直径为D,则待测电阻丝的电阻率ρ的计算式为ρ=$\frac{{πD}_{\;}^{2}}{4L}(\frac{U}{I}{-R}_{0}^{\;})$.
若用如图所示的电路完成 实验,如果两电表的读数分别为U和I,测得拉直后电阻丝的长度为L、直径为D,则待测电阻丝的电阻率ρ的计算式为ρ=$\frac{{πD}_{\;}^{2}}{4L}(\frac{U}{I}{-R}_{0}^{\;})$.