��Ŀ����
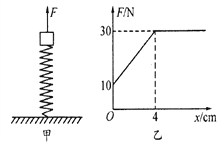
����Ŀ������ͼ��ʾ������ΪM�ij����龲ֹ�ڹ⻬ˮƽ�����ϣ���˹̶�һ����ϵ��Ϊk���㹻����ˮƽ���ʵ��ɣ��Ҳ���һ�����쳤��ϸ����������ֱǽ�ϣ�ϸ�����ܳ��ܵ��������ΪFr��ʹһ����Ϊm�����ٶ�Ϊv0��С���壬�ڻ�������Ħ������������ѹ�����ɣ����ɵĵ������ܱ���ʽΪ![]() (kΪ���ɵľ���ϵ����xΪ���ɵ��α�������
(kΪ���ɵľ���ϵ����xΪ���ɵ��α�������
��1������ϸ�������ϵ�������
��2����������ϸ�����Ϻ��ٵĹ����У����ܻ�õ��������ļ��ٶ�Ϊ���

���𰸡���1��v0>![]() ����2��
����2��![]()
��������
(1)�赯��ѹ����Ϊʱx1�������ϣ�![]()
�ӳ�ʼ״̬��ѹ���������ϵĹ����У�![]()
��ϸ�������ϵ�����Ϊ:![]()
��2������������˲�䣬С������ٶ�Ϊv1����![]()
���:![]()
������ѹ�������ʱ������������������ٶ�am��
ʱ���赯��ѹ����Ϊx2��С����ͻ�������ͬ���ٶ�Ϊv2,���������Ϻ���ѹ�������ʱ��С����ͻ��飬����ϵͳ�Ķ����غ㣬��е���غ㣺![]()
![]()
��ţ�ٵڶ����ɣ�![]()
���:![]()

��ϰ��ϵ�д�
�����Ŀ