题目内容
18. 如图所示,两根足够长、电阻不计的平行金属导轨相距L=0.5m,导轨平面与水平面成θ=37°角,导轨下端连接阻值R=2Ω的电阻,磁感应强度B=0.8T的匀强磁场方向垂直于导轨平面.一根质量m=0.2kg的导体棒ab放在两导轨上,在导轨之间的有效电阻r=2Ω,棒与导轨垂直并保持良好接触,导体棒与金属导轨间的动摩擦因数μ=0.5,重力加速度g=10m/s2,sin37°=0.6,求:
如图所示,两根足够长、电阻不计的平行金属导轨相距L=0.5m,导轨平面与水平面成θ=37°角,导轨下端连接阻值R=2Ω的电阻,磁感应强度B=0.8T的匀强磁场方向垂直于导轨平面.一根质量m=0.2kg的导体棒ab放在两导轨上,在导轨之间的有效电阻r=2Ω,棒与导轨垂直并保持良好接触,导体棒与金属导轨间的动摩擦因数μ=0.5,重力加速度g=10m/s2,sin37°=0.6,求:(1)导体棒沿导轨由静止开始下滑时的加速度大小;
(2)导体棒做匀速运动时的速度大小;
(3)从导体棒静止开始沿导轨下滑到刚好开始做匀速运动的过程中,电阻R上产生的焦耳热量Q=1J,则这个过程中导体棒的位移多大?
分析 (1)由牛顿第二定律可以求出加速度.
(2)导体棒匀速运动,处于平衡状态,由平衡条件可以求出匀速运动时的速度.
(3)由动能定理可以求出导体棒的位移.
解答 解:(1)金属棒开始下滑的初速为零,
由牛顿第二定律得:mgsinθ-μmgcosθ=ma,解得:a=2m/s2;
(2)设金属棒运动达到稳定时,设速度为v,所受安培力为F,
棒沿导轨方向受力平衡,由物体平衡条件得:
mgsinθ-μmgcosθ=F,解得:F=0.4N,
安培力:F=BIL=$\frac{{B}^{2}{L}^{2}v}{R+r}$,解得:v=10m/s;
(3)由动能定理得:mgssin37°-μmgcos37°s-W安=$\frac{1}{2}$mv2,
电阻R上产生的焦耳热量等于1J,则r上产生的焦耳热为1J,
则克服安培力做功:W安=2J,解得:s=30m
答:(1)金属棒沿导轨由静止开始下滑时的加速度为2m/s2;
(2)导体棒做匀速运动时的速度大小为10m/s;
(3)这个过程中导体棒ab的位移大小为30m.
点评 电磁感应中导体切割引起的感应电动势在考试中涉及较多,应明确受力分析、功能关系等的灵活应用,注意平衡状态的处理.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
9.关于对自由落体运动的认识,下列说法正确的是( )
| A. | 自由落体运动是沿竖直方向的匀加速直线运动 | |
| B. | 亚里士多德认为“重物”和“轻物”下落的同样快 | |
| C. | 自由落体运动在开始连续的三个1s末的速度之比为1:3:5 | |
| D. | 自由落体运动在开始连续的三个2s内的位移之比为1:3:5 |
3.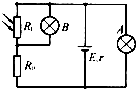 如图所示电路,电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的( )
如图所示电路,电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的( )
 如图所示电路,电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的( )
如图所示电路,电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的( )| A. | B灯变暗,A灯变亮 | B. | B灯变亮,A灯变暗 | C. | R0两端电压变大 | D. | 电源总功率变小 |
10. 如图所示为某磁谱仪部分构件的示意图,永磁铁提供匀强磁场,硅微条径迹探测器可以探测粒子在其中运动的轨迹.宇宙射线中有大量的电子、正电子和质子,当这些粒子从上部垂直进入磁场时,下列说法正确的是( )
如图所示为某磁谱仪部分构件的示意图,永磁铁提供匀强磁场,硅微条径迹探测器可以探测粒子在其中运动的轨迹.宇宙射线中有大量的电子、正电子和质子,当这些粒子从上部垂直进入磁场时,下列说法正确的是( )
 如图所示为某磁谱仪部分构件的示意图,永磁铁提供匀强磁场,硅微条径迹探测器可以探测粒子在其中运动的轨迹.宇宙射线中有大量的电子、正电子和质子,当这些粒子从上部垂直进入磁场时,下列说法正确的是( )
如图所示为某磁谱仪部分构件的示意图,永磁铁提供匀强磁场,硅微条径迹探测器可以探测粒子在其中运动的轨迹.宇宙射线中有大量的电子、正电子和质子,当这些粒子从上部垂直进入磁场时,下列说法正确的是( )| A. | 电子与正电子的偏转方向可能相同 | |
| B. | 电子与正电子在磁场中运动轨迹的半径一定相同 | |
| C. | 仅依据粒子运动轨迹无法判断该粒子是质子还是正电子 | |
| D. | 粒子的动能越大,它在磁场中运动轨迹的半径越小 |
3. 一斜面体固定在水平面上,斜面的倾角为θ,物体的质量为m,如图甲所示,在沿斜面向上的力F作用下,物体沿斜面向上做匀速运动;如图乙所示,在沿斜面向下的力$\frac{F}{9}$作用下,物体沿斜面向下做匀速运动,则物体与斜面间的动摩擦因数为( )
一斜面体固定在水平面上,斜面的倾角为θ,物体的质量为m,如图甲所示,在沿斜面向上的力F作用下,物体沿斜面向上做匀速运动;如图乙所示,在沿斜面向下的力$\frac{F}{9}$作用下,物体沿斜面向下做匀速运动,则物体与斜面间的动摩擦因数为( )
 一斜面体固定在水平面上,斜面的倾角为θ,物体的质量为m,如图甲所示,在沿斜面向上的力F作用下,物体沿斜面向上做匀速运动;如图乙所示,在沿斜面向下的力$\frac{F}{9}$作用下,物体沿斜面向下做匀速运动,则物体与斜面间的动摩擦因数为( )
一斜面体固定在水平面上,斜面的倾角为θ,物体的质量为m,如图甲所示,在沿斜面向上的力F作用下,物体沿斜面向上做匀速运动;如图乙所示,在沿斜面向下的力$\frac{F}{9}$作用下,物体沿斜面向下做匀速运动,则物体与斜面间的动摩擦因数为( )| A. | $\frac{5}{4}$cotθ | B. | $\frac{4}{5}$cotθ | C. | $\frac{5}{4}$tanθ | D. | $\frac{4}{5}$tanθ |
 有人想水平地夹持一叠书,他用手在这叠书的两端加一压力F=200N,如图所示,如每本书的质量为1kg,手与书之间的动摩擦因数为0.6,书与书之间的动摩擦因数为0.40,认为最大静摩擦力等于滑动摩擦力,g取10m/s2.则此人可能夹持书的最大数目为多少?
有人想水平地夹持一叠书,他用手在这叠书的两端加一压力F=200N,如图所示,如每本书的质量为1kg,手与书之间的动摩擦因数为0.6,书与书之间的动摩擦因数为0.40,认为最大静摩擦力等于滑动摩擦力,g取10m/s2.则此人可能夹持书的最大数目为多少? 某同学做“探究弹力和弹簧伸长的关系”的实验
某同学做“探究弹力和弹簧伸长的关系”的实验