��Ŀ����
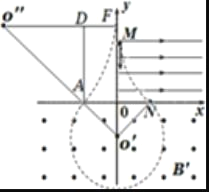
����Ŀ����ͼ��ʾ��ֽ������һֱ������ϵxOy���ڵ�һ����������x��������ǿ��СΪE����ǿ�糡���ڵڶ��������Ǵ�ֱ��ֽ���������ǿ�ų�B����Сδ֪�����ڵ����������������Ǵ�ֱ��ֽ���������ǿ�ų�B������Сδ֪����һ����Ϊm�������Ϊe�������Ӵ�������y���M�����ٶ�v0��MO�����������x���ϵ�N�����������ޣ������x�Ḻ����N���㣨��N�����O��Գƣ�����ڶ����ޣ����ǡ������y����������ٶȴ���y���������ϣ���֪tan��OMN=1/2�������������ƣ�����

(1)M��O�����l��O��N�����d��
(2)![]() ��ֵ��
��ֵ��
���𰸡�(1)![]() ��
��![]() ��(2)
��(2)![]()
��������
(1)�����ڵ糡������ƽ���˶���Ӧ����ƽ���˶����ɿ������l��d��
(2)�����ڴų���������Բ���˶������������ṩ�����������������˶��켣������ӹ���뾶��Ӧ��ţ�ٵڶ���������Ÿ�Ӧǿ�ȣ�Ȼ������Ÿ�Ӧǿ����
�����˶��켣��ͼ��������ʾ
(1) ������֪����֪tan��OMN=![]() ����O��N��ľ��룺d=
����O��N��ľ��룺d=![]() ��
��
���Ӵ�M�㵽N������ƽ���˶���d=![]() at12=
at12=![]() t12��l=v0t1��
t12��l=v0t1��
��ã�l=![]() ��d=
��d=![]() ��
��
(2) �����ڴų���������Բ���˶������ӽ���ų�ʱ�ٶȷ�����y�Ḻ�����н�Ϊ�ȣ�
��tan��=2tan��OMN=1����ã���=45�㣬
�ɼ���֪ʶ�ã������ڴų�B������Բ���˶��Ĺ���뾶��r��=![]() d��
d��
�����ڴų�B��������Բ���˶��Ĺ���뾶Ϊr��
�ɼ���֪ʶ�ã�Բ�Ľǣ���=��=45�㣬
cos��=![]() ����ã�r=��2+
����ã�r=��2+![]() ��d��
��d��
������Բ���˶����������ṩ��������
��ţ�ٵڶ����ɵã�evB��=m![]() ��evB=m
��evB=m![]() ��
��
��ã�![]() =��
=��![]() ��1����
��1����

����Ŀ�������õ��ڲⶨ�������ٶ�����ʵ���У�
��1��ijͬѧ�ֱ�ѡ�����ֲ��ϲ�ͬ��ֱ����ͬ��ʵ������ʵ�飬����ʵ��IJ����������¡���Ҫ���㵱�ص��������ٶ�ֵ��Ӧѡ�õ�________��ʵ�����ݡ�
��� | ������� | �ڳ�L/m | ���ڽ� | ȫ����N/�� |
1 | ͭ | 0.40 | 15�� | 20 |
2 | �� | 1.00 | 5�� | 50 |
3 | �� | 0.40 | 15�� | 10 |
4 | ľ | 1.00 | 5�� | 50 |
��2������ʵ���У������n ��ȫ��ʱ��Ϊt���ú��̶ȳ߲�õİ��߳������㵽�����϶˵ľ��룩Ϊ L���ÿ̶ȳ߲�ð����ֱ��Ϊ d. �������������ķ���д�����������ٶȵ�һ�����ʽ g��_____��
��3��ʵ����ijͬѧ���ֲ�õ��������ٶȵ�ֵ����ƫ������ԭ���п��ܵ�����_____����
A��ʵ���Ҵ��ڸ�ɽ�ϣ����뺣��̫��
B���������õİ�������̫����
C��ʵ�ʲ�� n ��ȫ��ʱ�� t������Ϊ��n��l����ȫ��ʱ��
D�����߳���Ϊ�ڳ�������
��4����ͬѧѡ���˺�����ʵ��װ�ú��������鲻ͬ�ڳ�L������T����ֵ��������ͼT2��Lͼ���е�ʵ��OM�������ͼ�ߵ�б��Ϊk���ص��������ٶ�g��________��
��5����ͬѧҲ���������ͬѧͬ����ʵ�飬��ʵ��������ֲ����ڳ�ʱ���˼��ϰ���İ뾶�����ͬѧ������T2��Lͼ��Ϊ��_________��

A.���ߢ٣���ƽ��OM B.���ߢڣ�ƽ��OM
C.���ߢۣ�ƽ��OM D.���ߢܣ���ƽ��OM