题目内容
如图所示，质量为m，带电量为q的小球以初速v0从斜面上水平抛出，并落在斜面上．已知斜面倾角为θ，重力加速度为g，空间存在着方向水平向右的匀强电场，场强大小为E．求小球运动过程中离斜面的最远距离以及离出发点的最远距离各是多少？
； （2）
将受到的力及初速度都沿斜面方向和垂直于斜面方向进行正交分解．
垂直斜面方向：合外力F1=mgcosθ-Eqsinθ，方向垂直斜面向下；
加速度a1=F1/m，方向垂直斜面向下．
初速度v1=v0sinθ，方向垂直斜面向上．
沿斜面方向：合外力F2=mgsinθ-Eqcosθ，方向沿斜面向下；
加速度a2=F2/m，方向沿斜面向下．
初速度v2=v0cosθ，方向沿斜面向下．
离斜面最远的时刻即为该方向的分速度减为0的时刻，可得离斜面的最远距离
．
离出发点的最远距离就是沿斜面方向运动的最大距离，s=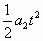
，式中t为在空中运动的时间，t=2v1/a1，代入解出．
垂直斜面方向：合外力F1=mgcosθ-Eqsinθ，方向垂直斜面向下；
加速度a1=F1/m，方向垂直斜面向下．
初速度v1=v0sinθ，方向垂直斜面向上．
沿斜面方向：合外力F2=mgsinθ-Eqcosθ，方向沿斜面向下；
加速度a2=F2/m，方向沿斜面向下．
初速度v2=v0cosθ，方向沿斜面向下．
离斜面最远的时刻即为该方向的分速度减为0的时刻，可得离斜面的最远距离
．离出发点的最远距离就是沿斜面方向运动的最大距离，s=
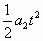，式中t为在空中运动的时间，t=2v1/a1，代入解出．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
加速后垂直进入偏转电场，离开偏转电场时的偏转量为
，两平行板间的距离为
，电势差为
，板长为
，为了提高示波管的灵敏度（单位偏转电压引起的偏转量
）可采取哪些措施？
，YY’和XX’两极板间的距离均为d。YY’和XX’紧密相连，不计它们间的间隙。水平偏转极板XX’端到荧光屏的距离为D。如果在偏转极板XX’上不加电压，偏转析板YY’上也不加电压，电子将打到荧光屏上中点O（即坐标轴的坐标原点）。如果在偏转极板XX’上不加电压，只在偏转极板YY’上加一电压Uy（正值），电子将打到荧光屏y轴上正方向某一点，求光点的y坐标值。
