题目内容
如图所示,质量为m1、带有正电荷q的金属小球和质量为m2、不带电的小木球之间用绝缘细线相连,置于竖直向上、场强为E、范围足够大的匀强电场中,两球恰能以速度v匀速竖直上升.当小木球运动到A点时细线突然断开,小木球运动到B点时速度为零,重力加速度为g,则( ) 
A.小木球的速度为零时,金属小球的速度大小为
B.小木球从点A到点B的过程中,A、B组成的系统,机械能在增加
C.A、B两点之间的电势差为
D.小木球从点A到点B的过程中,小木球动能的减少量等于两球重力势能的增量,而电场力对金属小球所做的功等于金属小球的机械能增加量
BC
解析试题分析:取向上为正方向,将AB看成一系统,由于系统匀速上升,所以系统在竖直方向合外力为零,系统的动量守恒,有: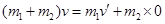 ,解得:
,解得: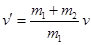 ,故选项A错误;此系统受重力之外,还有电场力做正功,所以系统的机械能增加,故选项B正确;剪断细线后,小木球向上做匀减速直线运动,由
,故选项A错误;此系统受重力之外,还有电场力做正功,所以系统的机械能增加,故选项B正确;剪断细线后,小木球向上做匀减速直线运动,由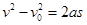 可知:
可知: ,由
,由 可知
可知 ,故选项C正确;从A到B运动过程中,对小木球仅受重力,故机械能守恒,即减少的动能转为重力势能,故选项D错误.
,故选项C正确;从A到B运动过程中,对小木球仅受重力,故机械能守恒,即减少的动能转为重力势能,故选项D错误.
考点:本题综合考查了动量守恒定律、机械能守恒定律和运动学规律的应用.

 阅读快车系列答案
阅读快车系列答案质量为m的小球,以速度v斜向上抛离高为H的桌面,如图.取桌面为零势面,那么小球经过离地高度为h的A点时所具有的机械能是
A.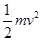 +mg(H-h) +mg(H-h) | B.mgH+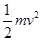 |
C.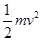 | D.mgH |
如图所示一轻质弹簧下端悬挂一质量为m的小球,用手托着,使弹簧处于原长,放手后,弹簧被拉至最大形变过程中,下列说法正确的是( )
| A.小球先失重后超重 |
| B.小球机械能守恒 |
| C.小球所受的重力做的功大于弹簧的弹力对小球所做的功 |
| D.弹簧被拉至最大形变时,弹簧的弹性势能、小球的重力势能之和最大 |
如图所示,弹簧的一端固定在竖直墙上,质量为m的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接,一个质量也为m的小球从槽高h处开始下滑,则( )
| A.在以后的运动过程中,小球和槽的动量始终守恒 |
| B.在下滑过程中小球和槽之间的相互作用力始终不做功 |
| C.被弹簧反弹后,小球和槽的机械能守恒,小球能回到槽高h处 |
| D.被弹簧反弹后,小球和槽都做速率不变的直线运动 |
如图所示,固定曲面AC是一段半径为4.0米的光滑圆弧形成的,圆弧与水平方向相切于A点,AB=10cm,现将一小物体先后从圆弧顶端C和中点D处由静止释放,到达曲面低端时速度分别为v1和v2,所需时间为t1和t2,以下说法正确的是( )
| A.v1 > v2 , t1= t2 | B.v1 > v2 , t1 > t2 |
| C.v1 < v2 , t1= t2 | D.v1 < v2 , t1 > t2 |
物体做下列几种运动,其中物体的机械能守恒的是
| A.平抛运动 |
| B.竖直方向上做匀速直线运动 |
| C.水平方向上做匀变速直线运动 |
| D.竖直平面内做匀速圆周运动 |
如图所示,小球以初速度为v0从光滑斜面底部向上滑动,恰能到达最大高度为h的斜面顶部.图中①是内轨半径大于h的光滑轨道,②是内轨半径小于h的光滑轨道,③是内轨直径等于h的光滑轨道,④是长为1/2h的轻杆(可绕固定点O转动,小球与杆的下端相碰后粘在一起).小球在底端时的初速度都为v0,则小球在以上四种情况中能到达高度h的是( )
| A.①③ | B.②④ | C.②③ | D.①④ |
当你骑自行车下坡时,虽然有空气阻力作用,你也没有蹬车,但车的速率越来越大, 在这个过程中,你和自行车的
| A.机械能守恒,减少的重力势能等于增加的动能 |
| B.机械能守恒,减少的重力势能大于增加的动能 |
| C.机械能不守恒,减少的重力势能小于增加的动能 |
| D.机械能不守恒,减少的重力势能大于增加的动能 |
 ,cos37°=
,cos37°=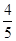 )
)