题目内容
【题目】如图所示,A、B 两物块的质量分别为 2m 和 m,静止叠放在水平地面上.A、B 间的动摩擦因数为μ,B 与地面间的动摩擦因数为 ![]() μ.最大静摩擦力等于滑动摩擦力,重力加速度为 g.现对 A 施加一水平拉力 F,则( )
μ.最大静摩擦力等于滑动摩擦力,重力加速度为 g.现对 A 施加一水平拉力 F,则( )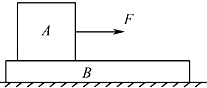
A.当 F<2 μmg 时,A,B 都相对地面静止
B.当 F= ![]() μmg 时,A 的加速度为
μmg 时,A 的加速度为 ![]() μg
μg
C.当 F>3 μmg 时,A 相对 B 滑动
D.无论 F 为何值,B 的加速度不会超过 ![]() μg
μg
【答案】B,C,D
【解析】解:A、B之间的最大静摩擦力为:fmax=μmAg=2μmg,A、B发生滑动的加速度为:a=μg,B与地面间的最大静摩擦力为:f′max= ![]() μ(mA+mB)g=
μ(mA+mB)g= ![]() μmg,设A、B相对滑动时的最小拉力为:F,由牛顿第二定律得:F﹣f′max=(m+2m)a,解得:F=
μmg,设A、B相对滑动时的最小拉力为:F,由牛顿第二定律得:F﹣f′max=(m+2m)a,解得:F= ![]() μmg;
μmg;
A、当 F<2μmg 时,f′max<F<fmax,AB之间不会发生相对滑动,B与地面间会发生相对滑动,所以A、B 都相对地面运动,A不符合题意.
B、当 F= ![]() μmg<
μmg< ![]() μmg时,故AB间不会发生相对滑动,由牛顿第二定律有:a=
μmg时,故AB间不会发生相对滑动,由牛顿第二定律有:a= ![]() =
= ![]() μg,B符合题意.
μg,B符合题意.
C、当F=3μmg< ![]() μmg 时,AB间会发生相对滑动,C符合题意.
μmg 时,AB间会发生相对滑动,C符合题意.
D、A对B的最大摩擦力为2μmg,无论F为何值,B的最大加速度为aB= ![]() =
= ![]() μg,当然加速度更不会超过
μg,当然加速度更不会超过 ![]() μg,D符合题意.
μg,D符合题意.
故答案为:BCD.
B物体所受的摩擦力由A物体提供,B物体的最大加速度不会大于A物体的,B物体所受的摩擦力最大为滑动摩擦力,当F小于B与地面间的最大静摩擦力两物体静止,F大于B与地面间的最大静摩擦力而小于A、B相对滑动时的最小拉力时,两物体一起运动。

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案【题目】如图所示,一倾角为37°的斜面固定在水平地面上,质量m=1kg的物体在平行于斜面向上的恒力F作用下,从A点由静止开始运动,到达B点时立即撤去拉力F.此后,物体到达C点时速度为零.每隔0.2s通过速度传感器测得物体的瞬时速度,下表给出了部分测量数据.(取 sin37°=0.6.cos37°=0.8)试求:
t/s | 0.0 | 0.2 | 0.4 | … | 2.2 | 2.4 | … |
v/ms﹣1 | 0.0 | 1.0 | 2.0 | … | 3.3 | 1.2 | … |
(1)斜面的摩擦系数μ;
(2)恒力F的大小;
(3)t=1.6s时物体的瞬时速度.