题目内容
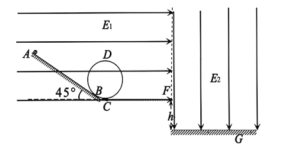
【题目】如图所示,光滑斜面轨道、粗糙水平轨道与半径![]() 的光滑圆轨道(所有轨道均为绝缘轨道)分别相切于B、C两点, D点为圆轨道最高点,此空间区域存在有场强大小为
的光滑圆轨道(所有轨道均为绝缘轨道)分别相切于B、C两点, D点为圆轨道最高点,此空间区域存在有场强大小为![]() 、方向水平向右的匀强电场,水平轨道末端F离水平地面高h=0.4m,F右侧的水平地面上方空间存在有场强大小为E
、方向水平向右的匀强电场,水平轨道末端F离水平地面高h=0.4m,F右侧的水平地面上方空间存在有场强大小为E![]() 、方向竖直向下的匀强电场。质量
、方向竖直向下的匀强电场。质量![]() 、电荷量
、电荷量![]() 的小钢球(可视为质点)由光滑斜面轨道上的A点静止释放。从B点进入圆轨道,C点离开圆轨道进入水平轨道,不计圆轨道在B、C间交错的影响。已知斜面轨道的倾角为θ=45°,小钢球与水平轨道间的动摩擦因数μ=0.5,重力加速度g=10m/s2,不计空气阻力。求:
的小钢球(可视为质点)由光滑斜面轨道上的A点静止释放。从B点进入圆轨道,C点离开圆轨道进入水平轨道,不计圆轨道在B、C间交错的影响。已知斜面轨道的倾角为θ=45°,小钢球与水平轨道间的动摩擦因数μ=0.5,重力加速度g=10m/s2,不计空气阻力。求:
(1)为保证小钢球能够在光滑圆环内做完整圆周运动,A、B两点间的竖直高度差至少为多少;
(2)若A、B两点间的竖直高度差为![]() m,小钢球到达D点时对轨道产生的压力大小;
m,小钢球到达D点时对轨道产生的压力大小;
(3)若把轨道所在区域的电场方向改为竖直向下,大小不变,且A点离水平轨道的高度为3.0m,水平轨道CF的长度为d= 1.0 m,小钢球通过轨道后落到水平地面的G点,求F、G两点间的水平距离。
【答案】(1)1.5 m(2)1.8N(3)2 m
【解析】
(1)小钢球在复合场中的等效重力加速度:
![]()
等效最低点与竖直方向的夹角为45°.
小钢球过等效最高点的最小速度
![]()
设A点离水平轨道CF的高度至少为H,如图所示:
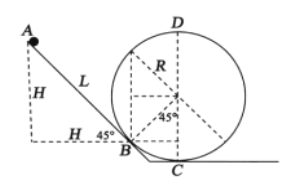
小钢球由A点静止释放运动到等效最高点,由动能定理:
![]()
联立解得:
H =1.5 m
(2)设小钢球运动到D点速度为vD,小钢球由A点静止释放运动到D点,由动能定理:
![]()
设在D点轨道对小钢球的压力为N,由牛顿第二定律有:
![]()
联立解得:
N=1.8N
由牛顿第三定律可知:对轨道压力N'=1.8N,方向竖直向下
(3)小钢球由A点静止释放运动到F点,由动能定理:
![]()
小钢球离开F后做类平抛运动:
![]()
![]()
![]()
联立解得:
x=2m