题目内容
【题目】物体甲乙都静止在同一水平面上,它们的质量为m甲、m乙 , 它们与水平面间的摩擦因数分别为μ甲、μ乙 , 用平行于水平面的拉力F分别拉两物体,甲乙的加速度与拉力F的关系分别如图所示,由图可知( )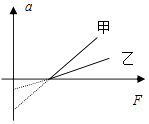
A.μ甲=μ乙m甲<m乙
B.μ甲<μ乙m甲>m乙
C.μ甲>μ乙m甲=m乙
D.μ甲>μ乙m甲<m乙
【答案】D
【解析】解:对质量为m的物体受力分析,假定动摩擦因素为μ,根据牛顿第二定律,有
F﹣μmg=ma
解得:
a= ![]() F﹣μg,
F﹣μg,
故a与F关系图象的斜率表示质量的倒数,故m甲<m乙;
从图象可以看出纵轴截距用表示﹣μg表示,故μ甲>μ乙;故D正确,ABC错误.
故选:D.
【考点精析】解答此题的关键在于理解滑动摩擦力的相关知识,掌握滑动摩擦力:利用公式f=μF N 进行计算,其中FN 是物体的正压力,不一定等于物体的重力,甚至可能和重力无关.或者根据物体的运动状态,利用平衡条件或牛顿定律来求解.

练习册系列答案
相关题目
【题目】某同学在探究小车速度随时间变化的规律时,对打出的一条纸带进行研究,从O点开始每5个打点作为一个计数点(中间4个打点未画出,电源频率为50赫兹),计数点分别为A、B、C、D、E,该同学已求出各计数点对应的速度,其数值见下表.(结果保留两位有效数字)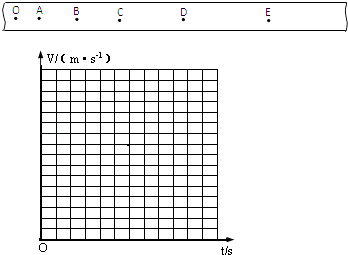
计数点 | A | B | C | D | E |
速度/(ms﹣1) | 0.70 | 0.91 | 1.10 | 1.30 | 1.49 |
(1)根据以上数据在所给的坐标纸中做出小车的v﹣t图线(适当标出横、纵坐标刻度).
(2)计数点O对应的速度为 m/s,加速度为m/s2 .