题目内容
 如图所示,静止在水平地面上的玩具小鸭质量m=0.5kg,受到与水平面夹角为53°的恒定拉力后,玩具开始沿水平地面运动.若拉力F=4.0N,经过时间t=2.0s,玩具移动距离为x=4.8m;撤去拉力F后,玩具又向前滑行一段距离.求:(sin53°=0.8,cos53°=0.6)
如图所示,静止在水平地面上的玩具小鸭质量m=0.5kg,受到与水平面夹角为53°的恒定拉力后,玩具开始沿水平地面运动.若拉力F=4.0N,经过时间t=2.0s,玩具移动距离为x=4.8m;撤去拉力F后,玩具又向前滑行一段距离.求:(sin53°=0.8,cos53°=0.6)(1)运动过程中,玩具的最大速度;
(2)撤去拉力后,玩具继续前进的距离.
分析:(1)玩具小鸭在拉力的作用下做匀加速运动,匀加速运动的末速度为玩具的最大速度,根据运动学公式求出玩具的加速度,然后根据速度时间公式求出玩具的最大速度.
(2)根据牛顿第二定律求出玩具的摩擦力和支持力,从而得出动摩擦因数.撤去拉力后,玩具在水平方向上仅受摩擦力,根据牛顿第二定律求出撤去拉力后的加速度,再根据匀变速直线运动的位移时间公式求出继续前进的距离.
(2)根据牛顿第二定律求出玩具的摩擦力和支持力,从而得出动摩擦因数.撤去拉力后,玩具在水平方向上仅受摩擦力,根据牛顿第二定律求出撤去拉力后的加速度,再根据匀变速直线运动的位移时间公式求出继续前进的距离.
解答:解:(1)由匀变速直线运动的位移时间公式得x=
a1t2
a1=2.4m/s2
vm=a1t=4.8m/s
故玩具的最大速度为4.8m/s.
(2)由牛顿第二定律得:F?cos53°-μN=ma1
F?sin53°+N=mg
联立两式 得μ=0.67
松手后玩具加速度a2=
=μg=6.7m/s2
滑行距离x2=
=1.7m
故玩具继续前进的距离为1.7m.
| 1 |
| 2 |
a1=2.4m/s2
vm=a1t=4.8m/s
故玩具的最大速度为4.8m/s.
(2)由牛顿第二定律得:F?cos53°-μN=ma1
F?sin53°+N=mg
联立两式 得μ=0.67
松手后玩具加速度a2=
| μmg |
| m |
滑行距离x2=
| ||
| 2a2 |
故玩具继续前进的距离为1.7m.
点评:解决本题的关键知道加速度是联系力学和运动学的桥梁,根据运动学求出加速度,再根据牛顿第二定律求出合力,从而得出未知力.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图所示,静止在水平地面上的物体质量为2kg,在水平恒力F推动下开始运动,4s末它的速度达到4m/s;此时将F撤去,物体又运动了16m停下来.如果物体与地面间的动摩擦因数不变,求:
如图所示,静止在水平地面上的物体质量为2kg,在水平恒力F推动下开始运动,4s末它的速度达到4m/s;此时将F撤去,物体又运动了16m停下来.如果物体与地面间的动摩擦因数不变,求: 如图所示,静止在水平桌面上的木块,在水平方向受到推力F1、F2和摩擦力.已知 F1=10N,F2=2N,若撤去F1,木块在水平方向上受到的合力为( )
如图所示,静止在水平桌面上的木块,在水平方向受到推力F1、F2和摩擦力.已知 F1=10N,F2=2N,若撤去F1,木块在水平方向上受到的合力为( ) (2006?嘉定区一模)如图所示,静止在水平地面上的斜面,倾角为θ,其上放一质量为m的物体,恰能自由匀速下滑,当用力F平行于斜面向下推物体加速运动时,地面对斜面的静摩擦力 f1=
(2006?嘉定区一模)如图所示,静止在水平地面上的斜面,倾角为θ,其上放一质量为m的物体,恰能自由匀速下滑,当用力F平行于斜面向下推物体加速运动时,地面对斜面的静摩擦力 f1=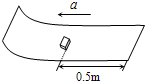 如图所示,静止在水平桌面的纸带上有一质量0.1kg的小铁块,它离纸带的右端距离为0.5m,铁块与纸带间动摩擦因数为0.1,现以2m/s2的加速度将纸带从铁块下抽出,问:(不计铁块大小,铁块不滚动)
如图所示,静止在水平桌面的纸带上有一质量0.1kg的小铁块,它离纸带的右端距离为0.5m,铁块与纸带间动摩擦因数为0.1,现以2m/s2的加速度将纸带从铁块下抽出,问:(不计铁块大小,铁块不滚动)