题目内容
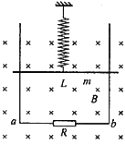
【题目】如图所示,在倾角为θ = 30°的斜面上,固定一宽度L = 0.2m的平行光滑金属导轨,在导轨上端接入电源和滑线变阻器,电源电动势E = 3.0V,内阻r = 1.0Ω。一质量m = 0.02kg的金属杆ab与两导轨垂直并接触良好,当滑线变阻器接入电路的阻值为R时,ab中电流大小I = 0.5A,此时杆恰好静止在导轨上。整个装置处于竖直向上的匀强磁场中,导轨与金属棒的电阻不计,取g = 10 m/s2。求:

(1)R的大小;
(2)磁感应强度B的大小;
(3)若只改变磁场,使金属杆ab仍静止在轨道上面,求磁感应强度的最小值和方向。
【答案】(1)5![]() (2)
(2)![]() T (3)1T 方向垂直斜面向上
T (3)1T 方向垂直斜面向上
【解析】
(1)根据欧姆定律求出滑动变阻器R接入电路中的阻值。
(2)金属杆受到重力、安培力和导轨的支持力而处于平衡状态。根据平衡条件,列方程求出安培力;金属杆与磁场方向垂直,根据安培力公式F=BIL,求出磁感应强度。
(3)当安培力的方向沿斜面向上时,磁感应强度最小,结合共点力平衡即可求出。
(1)设滑动变阻器接入电路的阻值为R,根据闭合电路欧姆定律得:E=I(R+r)
解得:R=5Ω
(2)金属杆静止在金属导轨上受到重力、支持力和水平方向的安培力,由受力平衡,
mgtan30°= BIL
代入数据得得:B=![]() T
T
(3)当安培力的方向沿斜面向上时,磁感应强度最小,设此时磁感应强度为B′,则:
mgsin300=B′IL
代入数据可得:B′=1T

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目