题目内容
10. 如图所示,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直地撞击在倾角θ=30°的斜面上,求:
如图所示,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直地撞击在倾角θ=30°的斜面上,求:(1)物体飞行的时间是多少?
(2)撞击时的速度大小.
分析 小球垂直地撞在倾角θ为30°的斜面上,知小球的速度方向与斜面垂直,将该速度进行分解,根据水平方向上的速度求出竖直方向上的分速度,根据竖直方向上做自由落体运动求出物体飞行的时间.根据平行四边形定则求出撞击时的速度大小.
解答 解:小球撞在斜面上的速度与斜面垂直,将该速度分解,如图.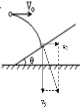
则tan60°=$\frac{{v}_{y}}{{v}_{0}}$,
解得${v}_{y}=\sqrt{3}{v}_{0}=10\sqrt{3}m/s$,
则飞行的时间t=$\frac{{v}_{y}}{g}=\frac{10\sqrt{3}}{10}s=\sqrt{3}s$.
(2)根据平行四边形定则知,撞击时的速度大小v=$\frac{{v}_{0}}{sin30°}=\frac{10}{\frac{1}{2}}m/s=20m/s$.
答:(1)物体飞行的时间是$\sqrt{3}s$;
(2)撞击时的速度大小为20m/s.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,根据竖直方向上的分速度求出运动的时间.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
20. 长度为L=1.6m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
长度为L=1.6m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
 长度为L=1.6m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
长度为L=1.6m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )| A. | 22.5N的压力 | B. | 7.5N的压力 | C. | 7.5N的拉力 | D. | 22.5N的拉力 |
1.关于机械振动和机械波的说法正确的是( )
| A. | 没有机械振动就没有机械波 | B. | 没有机械波就没有机械振 | ||
| C. | 振动是波的成因,波是振动的传播 | D. | 波源停止振动时,波就停止传播 |
18.穿过一个电阻为2Ω的单扎闭合线圈的磁通量每秒均匀减小0.4Wb,则线圈中( )
| A. | 感应电动势为4V | B. | 感应电动势每秒减小0.4V | ||
| C. | 感应电流恒为0.2A | D. | 感应电流每秒减小0.2A |
15. 如图所示,验电器A与B的顶端各安装了一个上端开有小孔的金属圆筒,验电器B带有正电荷,用带有绝缘柄的金属小球C,在下列操作中能将B上的电荷尽量多的搬至A的是( )
如图所示,验电器A与B的顶端各安装了一个上端开有小孔的金属圆筒,验电器B带有正电荷,用带有绝缘柄的金属小球C,在下列操作中能将B上的电荷尽量多的搬至A的是( )
 如图所示,验电器A与B的顶端各安装了一个上端开有小孔的金属圆筒,验电器B带有正电荷,用带有绝缘柄的金属小球C,在下列操作中能将B上的电荷尽量多的搬至A的是( )
如图所示,验电器A与B的顶端各安装了一个上端开有小孔的金属圆筒,验电器B带有正电荷,用带有绝缘柄的金属小球C,在下列操作中能将B上的电荷尽量多的搬至A的是( )| A. | 把C与筒B的内壁接触后,再与筒A的内壁接触,重复多次 | |
| B. | 把C与筒B的内壁接触后,再与筒A的外壁接触,重复多次 | |
| C. | 把C与筒B的外壁接触后,再与筒A的内壁接触,重复多次 | |
| D. | 把C与筒B的外壁接触后,再与筒A的外壁接触,重复多次 |
2. 如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度如图所示.弹簧测力计示数FA、FB、FC、FD由大到小的排列顺序是( )
如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度如图所示.弹簧测力计示数FA、FB、FC、FD由大到小的排列顺序是( )
 如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度如图所示.弹簧测力计示数FA、FB、FC、FD由大到小的排列顺序是( )
如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度如图所示.弹簧测力计示数FA、FB、FC、FD由大到小的排列顺序是( )| A. | FB>FD>FA>FC | B. | FD>FC>FB>FA | C. | FD>FB>FA>FC | D. | FC>FD>FB>FA |
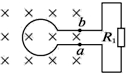 如图所示,面积为0.2m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=0.2tT,定值电阻R1=6Ω,线圈电阻R2=4Ω.求:
如图所示,面积为0.2m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=0.2tT,定值电阻R1=6Ω,线圈电阻R2=4Ω.求: