题目内容
如图（a）所示，“
”型木块放在光滑水平地面上，木块的水平表面AB粗糙，与水平面夹角θ＝37°的表面BC光滑。木块右侧与竖直墙壁之间连接着一个力传感器，当力传感器受压时，其示数为正值；当力传感器被拉时，其示数为负值。一个可视为质点的滑块从C点由静止开始下滑，物块在CBA运动过程中，传感器记录到的力和时间的关系如图（b）所示。滑块经过B点时无能量损失。（已知sin37°＝0.6，cos37°＝0.8，取g＝10m/s2。）求：
（1）斜面BC的长度L；
（2）滑块的质量m；
（3）运动过程中滑块克服摩擦力做的功W。
【答案】
（1）3m…（2）m＝2.5kg…（3）8m …
【解析】（1）分析滑块受力，
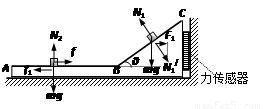
由牛顿第二定律得：
得：a1＝gsinq＝6m/s2…
通过图像可知滑块在斜面上运动时间为：t1＝1s…
由运动学公式得：L＝
a1t12＝3m…（4分）
（2）滑块对斜面的压力为：N1′＝mgcosq…
木板对传感器的压力为：F1＝N1′sinq…
由图像可知：F1＝12N…
解得：m＝2.5kg…（6分）
3）滑块滑到B点的速度为：v1＝a1t1＝6m/s…
由图像可知：f1＝5N，t2＝2s…
a2＝f/m＝2m/s2
s＝v1 t2－a2t22＝8m …(6分)
练习册系列答案
相关题目
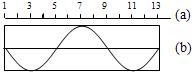在均匀媒质中，各点的平衡位置在同一直线上，相邻两质点间的距离均为a，如图（a）所示，振动由质点1向右传播，质点1开始振动的速度方向竖直向上，经过时间t，前13个质点第一次形成如图（b）所示的波形，则该波的周期是
一只小火箭放在某无大气层的星球表面的水平地面上，点火后在前5s时间内火箭受到的推力F的变化如图（a）所示，火箭速度变化如图（b）所示，不计火箭喷出气体的质量，则火箭在该星球表面由于星球的吸引而受到的重力是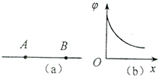
如图 （a）所示，AB是某电场中的一条电场线，若有一电子以某一初速度且仅在电场力的作用下，沿AB由点A运动到点B，所经位置的电势随距A点的距离变化的规律如图（b）所示．以下说法正确的是（ ）
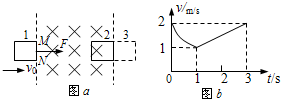如图（a）所示，在光滑水平面上用恒力F拉质量1kg的单匝均匀正方形铜线框，在1位置以速度v0=2m/s进入匀强磁场时开始计时t=0，此时线框中感应电动势0.8V，在t=3s时刻线框到达2位置开始离开匀强磁场．此过程中v-t图象如图（b）所示，那么恒力F的大小为