题目内容
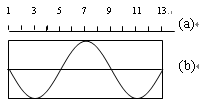
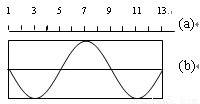
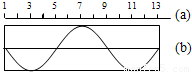
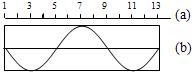在均匀媒质中，各点的平衡位置在同一直线上，相邻两质点间的距离均为a，如图（a）所示，振动由质点1向右传播，质点1开始振动的速度方向竖直向上，经过时间t，前13个质点第一次形成如图（b）所示的波形，则该波的周期是| t |
| 2 |
| t |
| 2 |
| 16a |
| t |
| 16a |
| t |
分析：简谐波向右传播，质点1的起始速度方向竖直向上，介质中各质点的起振方向都竖直向上，而图中质点13振动方向向下，说明波并不是刚传到质点13，根据前13个质点第一次形成如图（b）所示的波形，得到周期与时间的关系，求出周期，由图读出波长，求出波速．
解答：解：由波动图象读出波长为λ=8a．由题，波向右传播，质点1的起始速度方向竖直向上，介质中各质点的起振方向都向上，而图中质点13振动方向向下，说明波并不是刚传到质点13，已经振动了半个周期，则有2T=t，得到T=
．则波速为v=
=
．
故答案为：
，
．
| t |
| 2 |
| λ |
| T |
| 16a |
| t |
故答案为：
| t |
| 2 |
| 16a |
| t |
点评：本题容易犯的错误就是认为时间t=
T，得到T=
t，是由于对机械波特点：介质中各质点起振方向与波源起振方向相同掌握不牢造成的．
| 3 |
| 2 |
| 2 |
| 3 |
练习册系列答案
相关题目
