题目内容
【题目】一电视节目中设计了这样一个通关游戏:如图所示,光滑水平面上,某人乘甲车向右匀速运动,在甲车与静止的乙车发生弹性正碰前的瞬间,该人恰好抓住固定在他正上方某点的轻绳,当荡起至最高点速度为零时,松开绳子后又落到乙车中,并和乙车一起继续向前滑行。若人的质量m=56kg,甲车质量M1=10kg,乙车质量M2=40kg,甲车初速度v0=6m/s,求:
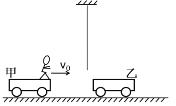
(1)最终人和乙车的速度;
(2)人落入乙车的过程中对乙车所做的功。
【答案】(1)v共=1.0 m/s;(2)W= -95.2J
【解析】
把该题分成几个过程,人在抓住绳子的过程中,对甲车的速度没有影响,甲车将于乙车发生弹性碰撞,由机械能守恒和动量守恒可求得甲乙两车碰撞后的速度,然后是人竖直的落到乙车上,人和乙车作用的过程中在水平方向上合外力为零,在水平方向上动量守恒,由动量守恒定律动量列式即可求得最终人和乙车的速度;
在人和乙车作用的过程中,人对乙车所做的功等于乙车的动能的变化,以乙车为研究对象,利用动能定理即可求得人落入乙车的过程中对乙车所做的功。
(1) 甲乙两车碰撞,在水平方向上动量守恒,设碰撞后甲车的速度为v1,乙车的速度为v2,选向右的方向为正,则有:
M1v0=M1v1+M2v2…①
碰撞过程中机械能守恒,有:![]() …②
…②
人松开绳子后做自由落体运动,与乙车相互作用使得过程中,在水平方向上合外力为零,动量守恒,设人和乙车的最终速度为v共,选向右的方向为正,有:
M2v2=(M人+M2)v共
代入数据解得:v共=1.0m/s;
(2) 人落入乙车的过程中对乙车所做的功,根据动能定理可知,即为乙车的动能的变化量,有:
![]() 。
。

练习册系列答案
相关题目