题目内容
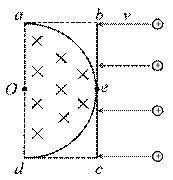
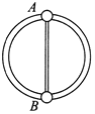
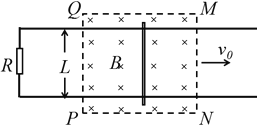
【题目】（1）如图所示，两条相距L的平行金属导轨位于同一水平面内，其左端接一阻值为R的电阻。矩形匀强磁场区域MNPQ的磁感应强度大小为B、方向竖直向下，质量为
的金属杆位于磁场区域内且静置在导轨上。现让磁场区域以速度
匀速向右运动，金属杆会在磁场力的作用下运动起来，已知金属杆运动时受到恒定的阻力f，除R外其它电阻不计，导轨光滑且足够长，杆在运动过程中与导轨垂直且始终未离开磁场区域。求：金属杆初始时的加速度和它能达到的最大速率
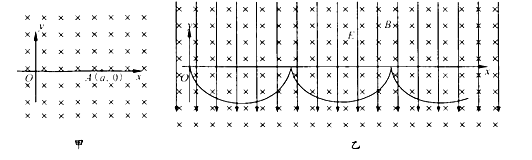
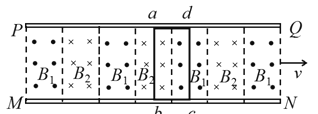
（2）根据（1）中的模型,某兴趣小组设计制作了一种磁悬浮列车模型，原理如图所示，PQ和MN是固定在水平地面上的两根足够长的平直导轨，导轨间分布着竖直（垂直纸面）方向等间距的匀强磁场B1和B2，二者方向相反。矩形金属框固定在实验车底部（车厢与金属框绝缘）。其中ad边宽度与磁场间隔相等，当磁场B1和B2同时以速度
沿导轨向右匀速运动时，金属框受到磁场力，并带动实验车沿导轨运动。已知金属框垂直导轨的ab边长
、总电阻
，列车与线框的总质量
， 
，悬浮状态下，实验车运动时受到恒定的阻力
。
①求实验车所能达到的最大速率；
②假设两磁场由静止开始向右做匀加速运动，当时间为
时，发现实验车正在向右做匀加速直线运动，此时实验车的速度为
，求由两磁场开始运动到实验车开始运动所需要的时间。
【答案】（1）
，方向水平向左； 
（2）①
②
【解析】试题分析：（1）根据牛顿第二定律可以求出加速度，当安培力与阻力相等时有最大速度，根据平衡条件即可求得；（2）为实现列车最终沿水平方向做匀加速直线运动，其加速度必须与两磁场由静止开始做匀加速直线运动的加速度相同，t时刻金属线圈中的电动势
，根据所受的安培力，结合牛顿第二定律求出列车最终的加速度．从磁场运动到列车起动需要时间为
．
（1）根据牛顿第二定律得： 
解得： 
，方向水平向左
杆最大速率
时，相对磁场的速率为
根据平衡条件有： 
解得： 
（2）①实验车最大速率为
时相对磁场的切割速率为
，
则此时线框所受的磁场力大小为
此时线框所受的磁场力与阻力平衡，得： 
解得： 
②根据题意分析可得，为实现实验车最终沿水平方向做匀加速直线运动，其加速度必须与两磁场由静止开始做匀加速直线运动的加速度相同，设加速度为
，
则t时刻金属线圈中的电动势 ： 
金属框中感应电流
又因为安培力
所以对试验车，由牛顿第二定律得
得
设从磁场运动到实验车起动需要时间为
，则
时刻金属线圈中的电动势
金属框中感应电流
又因为安培力
对实验车，由牛顿第二定律得： 
即
得： 
