Question

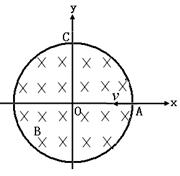
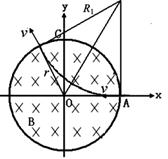
在以坐标原点O为圆心、半径为r的圆形区域内，存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场，一个不计重力的带电粒子从磁场边界与x轴的交点A处以速度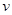沿-x方向射入磁场，它恰好从磁场边界与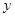轴的交点C处沿+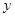方向飞出。

（1）请判断该粒子带何种电荷，并求出其比荷；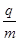

（2）若磁场的方向和所在空间范围不变，而磁感应强度的大小变为B₁，该粒子仍从A处以相同的速度射入磁场，但飞出磁场时的速度方向相对于入射方向改变了60⁰角，求磁感应强度B₁是多大？此次粒子在磁场中运动所用时间t是多少？

 

Answer 1

【答案】

解：（1）由粒子的飞行轨迹，利用左手定则可知，粒子带负电

粒子在磁场中做匀速圆周运动，由题意可知轨道半径R=r,

又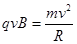，联立解得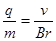

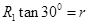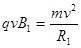（2）磁感应强度为B₁，粒子做圆周运动轨道半径设为R₁，依题意有又有，解得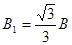,粒子在磁场中做圆周运动的周期为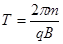,粒子在磁场中飞行的时间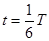,解得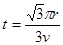

【解析】本题考查的是带电粒子在磁场中的运动问题。由左手定则先判断出带电粒子的运动轨迹，再根据带电粒子在磁场中的运动公式计算。