��Ŀ����
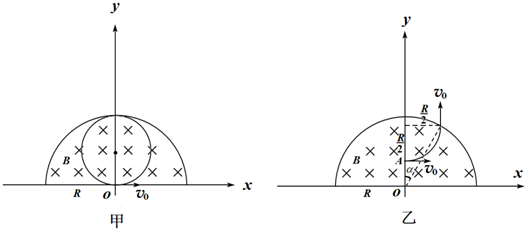
 ��ͼ��ʾ����������ԭ��OΪԲ�ģ��뾶ΪR�İ�Բ�������ڣ���һ�ų�����ֱ��xOy����ƽ�桢�Ÿ�Ӧǿ��ΪB����ǿ�ų���һ����������ӣ��������������ٶ�Ϊv0��ԭ��O��x���������ų�����������ǡ�ò��ܷɳ��ų�����
��ͼ��ʾ����������ԭ��OΪԲ�ģ��뾶ΪR�İ�Բ�������ڣ���һ�ų�����ֱ��xOy����ƽ�桢�Ÿ�Ӧǿ��ΪB����ǿ�ų���һ����������ӣ��������������ٶ�Ϊv0��ԭ��O��x���������ų�����������ǡ�ò��ܷɳ��ų�������1���ų��ķ�������ӵıȺɣ�
��2�������������ӵ������������y���ϵ�A�㣬�����������ٶ�v0ƽ��x����������ų�����Ҫ��������ų��������ͨ��y�ᣬ��OA�ľ�������Ϊ���٣�
��3�������������ӵ������������y���ϵ�M�㣬�Խ��������ٶ�v0ƽ��x����������ų�����֪��������ͨ���˴ų��߽��ϵ�P�㣬��P���xֵΪ+
| R | 4 |
��������1���ų��ķ��������ֶ����жϣ����⣬��������ǡ�ò��ܷɳ��ų���˵�����ӵĹ켣ǡ����ų��߽����У������켣�����ݼ���֪ʶ�õ��켣�İ뾶�����ɸ���ţ�ٵڶ�����������ӵıȺɣ�
��2����Ҫ��������ų��������ͨ��y�ᣬ���ڴų�������������˶��ķ�֮һ���ڣ������켣���ɼ���֪ʶ��⣮
��3�������켣��������ѧ֪ʶ����켣����Ӧ��Բ�ĽǦ�����t=
T���ʱ�䣮
��2����Ҫ��������ų��������ͨ��y�ᣬ���ڴų�������������˶��ķ�֮һ���ڣ������켣���ɼ���֪ʶ��⣮
��3�������켣��������ѧ֪ʶ����켣����Ӧ��Բ�ĽǦ�����t=
| �� |
| 2�� |
����⣺��1�������ֶ����֪����ǿ�ų��ĴŸ�Ӧǿ�ȵķ���ֱ��ֽ�����
�������ڴų�����������Բ���˶��İ뾶Ϊr�������У�R=2r ��
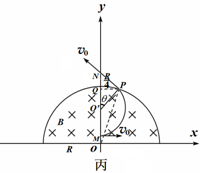
qBv0=m
��
��٢ڵã�
=
��
��2����Ҫ��������ų��������ͨ��y�ᣬ���ڴų�������������˶��ķ�֮һ���ڣ�����ͼ���У�
sin��=
=
����=30�� ��
�� OA=Rcos��-r ��
��ܢݵã�
OA=
R
��3���������ڴų�����������Բ���˶���Բ��ΪO�䣬��P��y�ᴹ�ߵô���ΪQ��ͼ���У�
sin��=
=
��
��� ��=
��
�������ڴų�����������Բ���˶������ں��˶�ʱ��ֱ�ΪT��t1��
T=
��
t1=
T ��
�����ӳ��ų����P��N�������˶�ʱ��Ϊt2��
tan��=
��
t2=
��
������M��N�˶���ʱ�� t=t1+t2
��ޢߢ���ã�t=
�𣺣�1����ǿ�ų��ĴŸ�Ӧǿ�ȵķ���ֱ��ֽ��������ӵıȺ�Ϊ
=
��
��2��OA�ľ�������Ϊ
R��
��3��������M��N�˶���ʱ��Ϊ
��
�������ڴų�����������Բ���˶��İ뾶Ϊr�������У�R=2r ��

qBv0=m
| ||
| r |
��٢ڵã�
| q |
| m |
| 2v0 |
| BR |
��2����Ҫ��������ų��������ͨ��y�ᣬ���ڴų�������������˶��ķ�֮һ���ڣ�����ͼ���У�
sin��=
| ||
| R |
| 1 |
| 2 |
�� OA=Rcos��-r ��
��ܢݵã�
OA=
| ||
| 2 |
��3���������ڴų�����������Բ���˶���Բ��ΪO�䣬��P��y�ᴹ�ߵô���ΪQ��ͼ���У�

sin��=
| ||
|
| 1 |
| 2 |
��� ��=
| �� |
| 6 |
�������ڴų�����������Բ���˶������ں��˶�ʱ��ֱ�ΪT��t1��
T=
| 2��r |
| v0 |
t1=
| ��-�� |
| 2�� |
�����ӳ��ų����P��N�������˶�ʱ��Ϊt2��
tan��=
| PN |
| r |
t2=
| PN |
| v0 |
������M��N�˶���ʱ�� t=t1+t2
��ޢߢ���ã�t=
(5��+2
| ||
| 12 |
| R |
| v0 |
�𣺣�1����ǿ�ų��ĴŸ�Ӧǿ�ȵķ���ֱ��ֽ��������ӵıȺ�Ϊ
| q |
| m |
| 2v0 |
| BR |
��2��OA�ľ�������Ϊ
| ||
| 2 |
��3��������M��N�˶���ʱ��Ϊ
(5��+2
| ||
| 12 |
| R |
| v0 |
���������⿼�������������ǿ�ų��е��˶���Ҫ����ס�뾶��ʽ�����ڹ�ʽ���������ӵ��˶��켣���ι�ϵ�ͱȽ������ˣ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ