题目内容
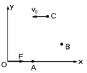
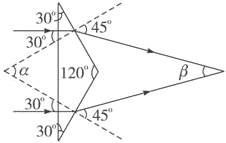
【题目】截面为等腰三角形的三棱镜，它的两个底角都为30°，棱镜的折射率为
．两条平行光线垂直于棱镜底面入射，如图所示，两条光线由棱镜射出时所成的角度为（ ）
A. 30° B. 60° C. 90° D. 120°
【答案】A
【解析】试题分析：作出光路图，由sinC=
求出棱镜的临界角．由几何知识得到两条光线射到右侧面时的入射角，由折射定律求出折射角．再根据几何知识求解两条光线由棱镜射出时所成的角度．
解：作出光路图．由棱镜材料的临界角：sinC==
=
，得C=45°，从题图由几何知识可知，光线从棱镜内射向另一侧面时的入射角i=30°＜C，所以光线从侧面折射出去，根据折射定律得
n=
，得sinr=nsini=
×sin30°=，则r=45°，
同理可知，第二条出射光线的折射角也是45°，
从图中的四边形可求出α=360°﹣120°﹣90°﹣90°=60°，
β=360°﹣135°﹣135°﹣α=90°﹣60°=30°，所以A正确．
故选A
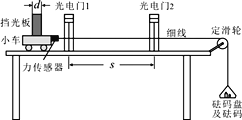
【题目】图甲中所示的装置可用来探究做功与速度变化的关系．倾角为θ的斜面体固定在实验台上，将光电门固定在斜面体的底端O点，将小球从斜面上的不同位置由静止释放．释放点到光电门的距离d依次为5cm、10cm、15cm、20cm、25cm、30cm．
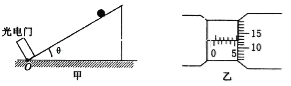
（1）用螺旋测微器测量钢球的直径，如图乙所示，钢球的直径D= cm
（2）该实验 （选填“需要”或者“不需要”）测量小球质量；小球通过光电门经历的时间为△t，小球通过光电门的速度为 （填字母），不考虑误差的影响，从理论上来说，该结果 （选填“＜”，“＞”或“=”）球心通过光电门的瞬时速度．
（3）为了探究做功与速度变化的关系，依次记录的实验数据如表所示．
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
d/×10﹣2m | 5.00 | 10.00 | 15.00 | 20.00 | 25.00 | 30.00 |
v/（ms﹣1） | 0.69 | 0.98 | 1.20 | 1.39 | 1.55 | 1.70 |
v2/（ms﹣1）2 | 0.48 | 0.97 | 1.43 | 1.92 | 2.41 | 2.86 |
| 0.83 | 0.99 | 1.10 | 1.18 | 1.24 | 1.30 |
从表格中数据分析能够得到关于“做功与速度变化的关系”的结论是： ．
