��Ŀ����
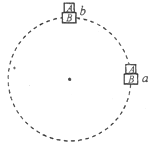
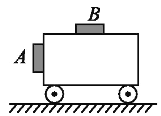
����Ŀ����ͼ��ʾ,��ȫ��ͬ��������A��B�ֱ�λ�����ʳ������ֱ���ˮƽ����,A��B�복���Ķ�Ħ��������Ϊ��,�����Ħ�������ڻ���Ħ����,�������ٶ�Ϊg.��С����ֹʱ,Aǡ�ò��»�.��ʹС�������˶�,Ϊ��֤A��B����,�� (����)
A. С�����ٶȿ�������,���ٶȿ�С����g
B. С���ļ��ٶ�һ������,���ܳ���(1+��)g
C. С���ļ��ٶ�һ������,���ܳ�����g
D. С���ļ��ٶ�һ������,���ܳ���(1+��)g
���𰸡�AD
��������
����С����ֹʱ��ǡ�ò��»����������������Ħ��������С������ʱ�����ݵ������������Ĺ�ϵ�ó����ٶȵķ���B������ץסB�����Ħ����������ٶȵ����ֵ��
�⣺С����ֹʱ��Aǡ�ò��»������Զ�A�У�mg=��F����
��С�������˶�ʱ��Ϊ�˱�֤A���»�����FN��F������FN��F��=ma������ʱ���ٶ�һ������B����
��B������mg+F����=mam�����am=��1+����g����A��D��ȷ��C����
��ѡ��AD��

��ϰ��ϵ�д�
�����Ŀ