题目内容
 在电场强度为E、方向水平向右的匀强电场中,有两个质量均为m的小球A、B(可被视为质点),被固定在一根绝缘轻杆的两端,轻杆可绕与电场方向垂直的固定转动轴O无摩擦转动,小球A、B与轴O间的距离分别为l、2l,其中小球B上带有电量为q的正电荷,小球A不带电,已知
在电场强度为E、方向水平向右的匀强电场中,有两个质量均为m的小球A、B(可被视为质点),被固定在一根绝缘轻杆的两端,轻杆可绕与电场方向垂直的固定转动轴O无摩擦转动,小球A、B与轴O间的距离分别为l、2l,其中小球B上带有电量为q的正电荷,小球A不带电,已知. |
| mg |
| ||
| 6 |
(1)小球B的电势能变化量的最大值(结果用m、g和l字母表示);
(2)轻杆转动到何位置时,小球A、B的速度达到最大?某同学这样解:目前轻杆无法平衡,在小球A、B的带动下,开始顺时针转动,当A、B的速度达到最大时,小球B所受的电场力与重力的合力恰与杆平行,如图(b)所示,所以tanθ=…,你认为这位同学的解法是否正确,若正确,请完成计算;若不正确,请说明理由,并用你自己的方法算出正确结果.
分析:(1)小球B电势能变化量为最大值时,小球的速度为0,根据动能定理求解;
(2)抓住小球A、B速度最大时,整个系统处于力矩平衡状态.
(2)抓住小球A、B速度最大时,整个系统处于力矩平衡状态.
解答:解:
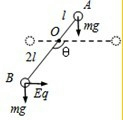
(1)小球B电势能变化量为最大值时,小球的速度为零,设轻杆转过的角度为θ,根据动能定理:
WGA+WGB+WF=△Ek
即:mg2lsinθ-mglsinθ-Eq2l(1-cosθ)=0
由已知
=
可得sinθ=
,cosθ=
即θ=120°
所以有△?max=|WF|=Eq2l(1-cosθ)=
mgl
(2)不正确
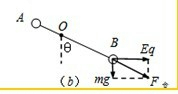
因为当小球A、B的速度达到最大时,整个系统处于力矩平衡状态
当系统处于力矩平衡时:MGA+M电=MGB
设此时轻杆与竖直方向夹角为θ,则
mglsinθ+Eq2lcosθ=2mglsinθ
解得tanθ=
即θ=30°
答:(1)小球B的电势能变化量的最大值为
mgl;
(2)tanθ=
即θ=30°

(1)小球B电势能变化量为最大值时,小球的速度为零,设轻杆转过的角度为θ,根据动能定理:
WGA+WGB+WF=△Ek
即:mg2lsinθ-mglsinθ-Eq2l(1-cosθ)=0
由已知
| Eq |
| mg |
| ||
| 6 |
可得sinθ=
| ||
| 2 |
| 1 |
| 2 |
所以有△?max=|WF|=Eq2l(1-cosθ)=
| ||
| 2 |
(2)不正确

因为当小球A、B的速度达到最大时,整个系统处于力矩平衡状态
当系统处于力矩平衡时:MGA+M电=MGB
设此时轻杆与竖直方向夹角为θ,则
mglsinθ+Eq2lcosθ=2mglsinθ
解得tanθ=
| ||
| 3 |
答:(1)小球B的电势能变化量的最大值为
| ||
| 2 |
(2)tanθ=
| ||
| 3 |
点评:解答本题要注意当小球A、B的速度达到最大时,整个系统处于力矩平衡状态,难度适中.

练习册系列答案
相关题目
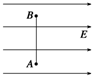 如图所示,在电场强度为E、方向水平向右的匀强电场中,A、B为一竖直线上的两点,相距为L,外力F将质量为m、带电荷量为q的粒子从A点匀速移到B点,重力不能忽略,则下列说法中正确的是( )
如图所示,在电场强度为E、方向水平向右的匀强电场中,A、B为一竖直线上的两点,相距为L,外力F将质量为m、带电荷量为q的粒子从A点匀速移到B点,重力不能忽略,则下列说法中正确的是( )| A、外力的方向水平向左 | ||
| B、外力的方向竖直向上 | ||
| C、外力的大小等于qE+mg | ||
D、外力的大小等于
|

