题目内容
(2012?闵行区三模)如图(a)所示,在电场强度为E、方向水平向右的匀强电场中,有两个质量均为m的小球A、B(可被视为质点),被固定在一根绝缘轻杆的两端,轻杆可绕与电场方向垂直的固定转动轴O无摩擦转动,小球A、B与轴O间的距离分别为l、2l,其中小球B上带有电量为q的正电荷,小球A不带电.将轻杆转动到水平方向后,无初速释放,若已知
=
.

求:(1)轻杆转动到何位置时,小球A、B的速率达到最大.
(2)若l=
米,小球A、B的最大速率为多少?
某同学是这样解的:(1)目前轻杆无法平衡,在小球A、B的带动下,开始顺时针转动,当A、B的速度达到最大时,小球B所受的电场力与重力的合力恰与杆平行,如图(b)所示,所以tanθ=qE/mg=…,
(2)对从a图位置到b图位置过程用动能定理求出A、B两球的最大速率.你认为这位同学的解法是否正确,若正确,请完成计算;若不正确,请说明理由,并用你自己的方法算出正确结果.
. |
| mg |
| ||
| 6 |

求:(1)轻杆转动到何位置时,小球A、B的速率达到最大.
(2)若l=
| 3 |
某同学是这样解的:(1)目前轻杆无法平衡,在小球A、B的带动下,开始顺时针转动,当A、B的速度达到最大时,小球B所受的电场力与重力的合力恰与杆平行,如图(b)所示,所以tanθ=qE/mg=…,
(2)对从a图位置到b图位置过程用动能定理求出A、B两球的最大速率.你认为这位同学的解法是否正确,若正确,请完成计算;若不正确,请说明理由,并用你自己的方法算出正确结果.
分析:(1)解题方法不正确,因为当小球A、B的速度达到最大时,整个系统处于力矩平衡状态.根据力矩平衡列式求解;
(2)对从a图位置到b图位置过程用动能定理即可求解.
(2)对从a图位置到b图位置过程用动能定理即可求解.
解答:解:(1)解题方法不正确
因为当小球A、B的速度达到最大时,整个系统处于力矩平衡状态.
当系统处于力矩平衡时:MGA+M电=MGB
设此时轻杆与竖直方向夹角为θ,则
mglsinθ+Eq2lcosθ=2mglsinθ
解得:tanθ=
θ=30°
(2)对从a图位置到b图位置过程用动能定理得:
2mglcos30°-mglcos30°-2qEsin30°=
mvA2+
m(2vA)2
解得:vA=2m/s
vB=2vA=4m/s
答:(1)轻杆转动到与竖直方向成30°时,小球A、B的速率达到最大.
(2)若l=
米,小球A的最大速率为2m/s,B的最大速率为4m/s.
因为当小球A、B的速度达到最大时,整个系统处于力矩平衡状态.
当系统处于力矩平衡时:MGA+M电=MGB
设此时轻杆与竖直方向夹角为θ,则
mglsinθ+Eq2lcosθ=2mglsinθ
解得:tanθ=
| ||
| 3 |
θ=30°
(2)对从a图位置到b图位置过程用动能定理得:
2mglcos30°-mglcos30°-2qEsin30°=
| 1 |
| 2 |
| 1 |
| 2 |
解得:vA=2m/s
vB=2vA=4m/s
答:(1)轻杆转动到与竖直方向成30°时,小球A、B的速率达到最大.
(2)若l=
| 3 |
点评:解答本题要注意当小球A、B的速度达到最大时,整个系统处于力矩平衡状态,难度适中.

练习册系列答案
相关题目
 (2012?闵行区三模)如图所示为“研究电磁感应现象”的实验装置,部分导线已连接.
(2012?闵行区三模)如图所示为“研究电磁感应现象”的实验装置,部分导线已连接.
 (2012?闵行区三模)约里奥?居里夫妇因发现人工放射性而获得了1935年的诺贝尔化学奖,他们发现的放射性元索
(2012?闵行区三模)约里奥?居里夫妇因发现人工放射性而获得了1935年的诺贝尔化学奖,他们发现的放射性元索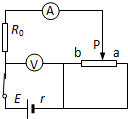 (2012?闵行区三模)如图所示电路中,电源的电动势为E,内电阻为r,当滑动变阻器的滑片P由a向b滑动的过程中,电流表、电压表的示数变化情况是( )
(2012?闵行区三模)如图所示电路中,电源的电动势为E,内电阻为r,当滑动变阻器的滑片P由a向b滑动的过程中,电流表、电压表的示数变化情况是( )