Question

【题目】如图所示，倾角θ＝37的粗糙传送带与光滑水平面通过半径可忽略的光滑小圆弧平滑连接，传送带始终以v＝3m/s的速率顺时针匀速转动，A、B、C滑块的质量分别为mA=1kg，mB=2kg，mC=3kg，（各滑块均可视为质点）．A、B间夹着质量可忽略的火药．k为处于原长的轻质弹簧，两端分别与B、C连接．现点燃火药（此时间极短且不会影响各物体的质量和各表面的光滑程度），滑块A以6m/s的速度水平向左冲出，接着沿传送带向上运动，已知滑块A与传送带间的动摩擦因数为μ＝0.75，传送带与水平面足够长，取g=10m/s2，sin37°=0.6，cos37°=0.8．

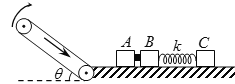
(1)计算滑块A沿传送带向上滑行的最大距离x；

(2)在滑块B、弹簧、滑块C相互作用的过程中，当弹簧第一次恢复原长时（此时滑块A还未追上滑块B），计算B、C的速度；

(3)若滑块A追上滑块B时能粘住，定量分析在A与B相遇的各种可能情况下，A、B、C及弹簧组成系统的机械能范围．（提示：因A、B相遇时，B的速度不可预知，故粘住后A、B、C及弹簧组成系统的机械能有各种可能值）

Answer 1

【答案】（1）1.5m（2）-0.6m/s;2.4m/s（3）

【解析】

（1）滑块A沿传送带向上的运动的过程

由动能定理有：

代入数据解得：x＝1.5m

（2）炸药爆炸过程，设B获得的速度为vB，对A、B系统

由动量守恒有：–mAvA＋mBvB＝0

解得：vB=3m/s

在B、C相互作用的过程中，设当弹簧第一次恢复原长时，B、C的速度分别为

由动量守恒有：

由能量守恒有：

解得：

（3）因滑动摩擦力f＝μmgcosθ＝6N，重力沿斜面向下的分力mgsinθ＝6N．所以A到达最高点后先反向加速，当速度达到3m/s后随传送带一起（相对传送带静止）返回光滑水平面

此时：

因A、B相遇时，B的速度不能确定，可能是–0.6m/s与3m/s间的任何值．

①当时，此时，机械能损失最大，系统机械能最小．设A、B粘连后的共同速度为v′．

由动量守恒有：

解得：v′=0.6m/s

系统机械能的最小值：

②当时，此时，机械能损失最小，

系统机械能的最大值

所以A、B、C及弹簧系统机械能范围：9.18J≤E≤13.5J