题目内容
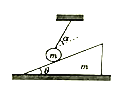
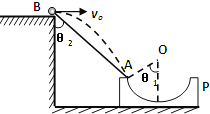
【题目】如图所示，P是水平面上的圆弧凹槽．从高台边B点以速度v0水平飞出的小球，恰能从固定在某位置的凹槽的圆弧轨道的左端A沿圆弧切线方向进入轨道．O是圆弧的圆心，θ1是OA与竖直方向的夹角，θ2是BA与竖直方向的夹角．则（ ）
A．cotθ1tanθ2=2
B．tanθ1tanθ2=2
C．cotθ1cotθ2=2
D．tanθ1cotθ2=2
【答案】B
【解析】
试题分析：从图中可以看出，速度与水平方向的夹角为θ1，位移与竖直方向的夹角为θ2．然后求出两个角的正切值．
解：平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动．速度与水平方向的夹角为θ1，
tan
．位移与竖直方向的夹角为θ2，
，则tanθ1tanθ2=2．故B正确，A、C、D错误．
故选B．
练习册系列答案
阅读快车系列答案
相关题目
