题目内容
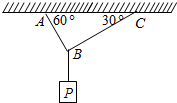 如图所示,用绳AB和BC吊起一重物P,AB绳和水平面AC间的夹角为60°,BC绳与AC间的夹角为30°,绳AB能承受的最大拉力为300N,绳BC能承受的最大拉力为200N,求物体P的最大许可重力.
如图所示,用绳AB和BC吊起一重物P,AB绳和水平面AC间的夹角为60°,BC绳与AC间的夹角为30°,绳AB能承受的最大拉力为300N,绳BC能承受的最大拉力为200N,求物体P的最大许可重力.分析:对结点受力分析后,应用平衡条件求解出AC绳和BC绳上的拉力关系,根据两绳所能承受的最大拉力判断谁先断,按照最小的求解即可.
解答:解:以结点为研究对象.设重物重力为G,绳子AB上拉力为T1,绳子BC上拉力为T2,受力分析如下图所示:
根据平衡条件和力的分解:T1=Gcos30°=300N,则G=200
N;
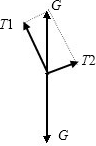
T2=Gsin30°=300N,则G=600N,
为保证绳子不断,物体P的重力应取较小值200
N
答:物体P最大许可重力为200
N.
根据平衡条件和力的分解:T1=Gcos30°=300N,则G=200
| 3 |

T2=Gsin30°=300N,则G=600N,
为保证绳子不断,物体P的重力应取较小值200
| 3 |
答:物体P最大许可重力为200
| 3 |
点评:对结点进行受力分析,运用力的合成或分解结合共点力平衡条件解决问题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
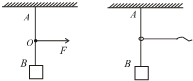 如图所示,轻绳AB能承受的最大拉力为100N,在它下面悬挂一重为50N的重物,通过能承受最大拉力为50N的绳子,分两种情况缓慢地拉起重物.第一次,绳子固定在O点,施加一水平方向的力F作用于绳子;第二次用拴有光滑小环的绳子,且绳子所能承受的最大拉力也为50N.绳子刚好断裂时,绳AB上部分与竖直方向的夹角分别为θ1和θ2,关于两者大小关系的说法中正确的是( )
如图所示,轻绳AB能承受的最大拉力为100N,在它下面悬挂一重为50N的重物,通过能承受最大拉力为50N的绳子,分两种情况缓慢地拉起重物.第一次,绳子固定在O点,施加一水平方向的力F作用于绳子;第二次用拴有光滑小环的绳子,且绳子所能承受的最大拉力也为50N.绳子刚好断裂时,绳AB上部分与竖直方向的夹角分别为θ1和θ2,关于两者大小关系的说法中正确的是( )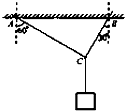 如图所示,用绳AC和BC吊起一个物体,绳AC与竖直方向的夹角为60°,绳BC与竖直方向的夹角为30°,两绳能承受的最大拉力均为100N,g=10m/s2,求:
如图所示,用绳AC和BC吊起一个物体,绳AC与竖直方向的夹角为60°,绳BC与竖直方向的夹角为30°,两绳能承受的最大拉力均为100N,g=10m/s2,求: 和
和 ,关于两者大小关系的说法中正确的是( )
,关于两者大小关系的说法中正确的是( )



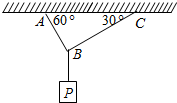 如图所示,用绳AB和BC吊起一重物P,AB绳和水平面AC间的夹角为60°,BC绳与AC间的夹角为30°,绳AB能承受的最大拉力为300N,绳BC能承受的最大拉力为200N,求物体P的最大许可重力.
如图所示,用绳AB和BC吊起一重物P,AB绳和水平面AC间的夹角为60°,BC绳与AC间的夹角为30°,绳AB能承受的最大拉力为300N,绳BC能承受的最大拉力为200N,求物体P的最大许可重力.