题目内容
【题目】如图所示,一水平方向的传送带以恒定速度v=2m/s沿顺时针方向匀速转动,传送带右端固定着一光滑的四分之一圆弧轨道,并与圆弧下端相切。一质量为m=1kg的物体自圆弧轨道的最高点由静止滑下,圆弧轨道的半径为R=0.45m,物体与传送带之间的动摩擦因数为μ=0.2,不计物体滑过圆弧轨道与传送带交接处时的能量损失,传送带足够长,g取10m/s2。求:
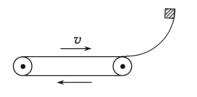
(1)物体第一次滑到圆弧轨道下端时,对轨道的压力大小FN;
(2)物体从第一次滑上传送带到离开传送带的过程中,摩擦力对传送带做的功W,以及由于摩擦而产生的热量Q。
【答案】(1)30N(2)-10J;12.5J
【解析】(1) 根据动能定理: ![]()
解得:v1=3m/s
在轨道最低点: ![]()
由牛顿第三定律FN=N=30N
(2) 物体从第一次滑上传送带到离开传送带的过程中,由定律定理: ![]() ,t=2.5s
,t=2.5s
摩擦力对传送带做的功 ![]()
![]()
摩擦而产生的热 ![]()

练习册系列答案
相关题目