题目内容
13．第一次下落阶段，弹簧绳被拉伸的过程中，小明下落速度大小的变化情况是（ ）| A． | 一直在增大 | B． | 先增大后减小 | C． | 先减小后增大 | D． | 一直在减小 |
分析 第一次下落阶段，弹簧绳被拉伸的过程中，弹力变大，对人进行受力分析，根据牛顿第二定律列式即可分析加速度的变化情况，根据加速度的方向和速度方向的关系，判断小明速度的变化情况．
解答 解：第一次下落阶段，弹簧绳被拉伸的过程中，根据牛顿第二定律得：a=$\frac{mg-F}{m}$．弹簧绳被拉伸的过程中，弹力变大，则加速度变小，方向向下，小明做加速度减小的加速运动，当弹力等于重力时，加速度为零，速度最大，
此后弹力继续增大，加速度方向向上，小明做加速度增大的减速运动，所以小明下落速度大小的变化情况是先增大后减小，故ACD错误，B正确．
故选：B．
点评 本题主要考查了牛顿第二定律的直接应用，要求同学们能正确对小明进行受力分析，知道加速度方向与速度方向相同时，做加速运动，相反时做减速运动．
练习册系列答案
相关题目
3．关于电场强度与电势的关系，下列说法正确的是（ ）
| A． | 场强相等的各点，电势也一定相等 | |
| B． | 电势为零的位置，场强也一定为零 | |
| C． | 电势降低的方向就是电场强度的方向 | |
| D． | 沿场强的反方向，电势逐渐升高 |
4．
在直角坐标系xOy中，x轴上方有磁感应强度为B的匀强磁场，在x轴下方有电场强度为E的匀强电场．从M点以一定的初速度水平射出一带正电粒子（不计重力）恰好经坐标原点O到达N，如图所示，已知M点的横坐标为-a，且MN两点关于坐标原点对称，粒子经O点时速度恰好与水平方向成45°角，则下列说法正确的是（ ）
在直角坐标系xOy中，x轴上方有磁感应强度为B的匀强磁场，在x轴下方有电场强度为E的匀强电场．从M点以一定的初速度水平射出一带正电粒子（不计重力）恰好经坐标原点O到达N，如图所示，已知M点的横坐标为-a，且MN两点关于坐标原点对称，粒子经O点时速度恰好与水平方向成45°角，则下列说法正确的是（ ）| A． | 粒子从M运动到O的时间与从O运动到N的时间相等 | |
| B． | 粒子在磁场中的轨道半径为$\sqrt{2}$a | |
| C． | M点的纵坐标为（$\sqrt{2}$-1）a | |
| D． | 粒子到达N点时的速度恰好水平 |
1．关于物质波，以下观点不正确的是（ ）
| A． | 只要是运动着的物体，不论是宏观物体还是微观粒子，都有相应的波与之对应，这就是物质波 | |
| B． | 只有运动着的微观粒子才有物质波，对于宏观物体，不论其是否运动，都没有相对应的物质波 | |
| C． | 由于宏观物体的德布罗意波长太小，所以无法观察到它们的波动性 | |
| D． | 电子束照射到金属晶体上得到了电子束的衍射图样，从而证实了德布罗意的假设是正确的 |
8．“西电东送”工程是缓解我国东部沿海城市能源紧张的有效措施，由西向东的远距离输电要采用高压电．关于高压输电的优点，下列说法中正确的是（ ）
| A． | 可根据需要调节交流电的频率 | B． | 可加快输电的速度 | ||
| C． | 可节省输电成本 | D． | 可减少输电线上的能量损失 |
18．
如图所示，轻质弹簧的一端与固定的竖直板P连接，另一端与物体A相连，弹簧处于水平状态；物体A置于光滑水平桌面上，A右端水平连接一细线，细线绕过光滑的定滑轮与物体B相连．开始时托住B，让系统处于静止状态且细线恰好伸直，然后由静止释放B，直至B获得最大速度（假设此过程中B未着地）．已知弹簧的劲度系数为k，A、B两物体的质量均为m，物体A始终处在水平桌面上，不计绳的伸长，重力加速度为g．下列说法正确的是（ ）
如图所示，轻质弹簧的一端与固定的竖直板P连接，另一端与物体A相连，弹簧处于水平状态；物体A置于光滑水平桌面上，A右端水平连接一细线，细线绕过光滑的定滑轮与物体B相连．开始时托住B，让系统处于静止状态且细线恰好伸直，然后由静止释放B，直至B获得最大速度（假设此过程中B未着地）．已知弹簧的劲度系数为k，A、B两物体的质量均为m，物体A始终处在水平桌面上，不计绳的伸长，重力加速度为g．下列说法正确的是（ ）| A． | 物体A与物体B组成的系统机械能守恒 | |
| B． | 当物体B获得最大速度时，弹簧伸长量为$\frac{2mg}{k}$ | |
| C． | 当物体B获得最大速度时，若弹簧的弹性势能增加量为$\frac{{{m^2}{g^2}}}{2k}$，则物体A的速度大小为$g\sqrt{\frac{m}{2k}}$ | |
| D． | 此过程中B物体机械能的减少量大于弹簧弹性势能的增加量 |
5．下列说法正确的是（ ）
| A． | 因为功有正负，所以功是矢量 | |
| B． | 功的大小只由力和位移决定 | |
| C． | 把重1N的物体匀速举高1m，克服重力做功为-1J | |
| D． | 做功的过程就是物体能量的转化过程 |
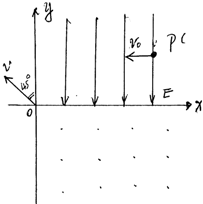如图所示，xy平面的第一象限内有沿负y方向的匀强电场，在第四象限内有垂直于纸面向外的匀强磁场，现有一质量为m，电量+q的粒子，以初速度v0沿负x方向坐标为（3l，l）的P点开始运动，接着进入磁场后从原点射出，射出的速度方向与y轴正方向夹角为45°，不计粒子重力，求：
如图所示，电路中的灯泡标有“0.1V，0.4W”，电源的电动势为4V，内阻为0.05Ω，电动机内阻为0.1Ω，此时灯泡与电动机都正常工作求：