题目内容
2. 如图所示,xy平面的第一象限内有沿负y方向的匀强电场,在第四象限内有垂直于纸面向外的匀强磁场,现有一质量为m,电量+q的粒子,以初速度v0沿负x方向坐标为(3l,l)的P点开始运动,接着进入磁场后从原点射出,射出的速度方向与y轴正方向夹角为45°,不计粒子重力,求:
如图所示,xy平面的第一象限内有沿负y方向的匀强电场,在第四象限内有垂直于纸面向外的匀强磁场,现有一质量为m,电量+q的粒子,以初速度v0沿负x方向坐标为(3l,l)的P点开始运动,接着进入磁场后从原点射出,射出的速度方向与y轴正方向夹角为45°,不计粒子重力,求:(1)粒子从0点射出时速度;
(2)电场强度大小;
(3)磁感应强度大小;
(4)从P点运动到0点所用时间t总.
分析 (1)由速度的合成法求出带电粒子刚进入磁场时的速度大小,即为粒子从O点射出磁场时的速度大小;带电粒子射入电场中作类平抛运动,带电粒子在磁场中由洛伦兹力提供向心力作匀速圆周运动,根据几何知识得到带电粒子进入磁场时速度方向与x轴夹角45°;
(2)粒子在电场中做类平抛运动,根据牛顿第二定律和运动学公式结合求出E的大小;
(3)由牛顿第二定律可以求出磁感应强度;
(4)电场中,由运动学公式和牛顿第二定律结合求时间.磁场中,根据轨迹的圆心角求出时间
解答 解:粒子运动轨迹如图所示:
(1)由对称性可知,粒子在Q点时速度大小为v,方向与-x轴方向成45°,
则:vcos45°=v0,
解得:v=$\sqrt{2}$v0,
(2)在P到Q的过程中,由动能定理得:qEl=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02,
联立以上两式解得:E=$\frac{m{v}_{0}^{2}}{2ql}$.
(3)由几何知识可知,r=$\frac{\sqrt{2}}{2}$l,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
解得:B=$\frac{2m{v}_{0}}{ql}$;
(4)粒子在电场中运动,到达Q点时沿-y方向速度大小为vy=v0,
P到Q的运动时间为:t1=$\frac{2l}{{v}_{0}}$,
水平分运动,有x=v0t,竖直分运动,有l=$\frac{{v}_{0}}{2}$t,则x=2l.
带电粒子在磁场中运动,其轨道半径:R=$\frac{mv}{qB}$=$\frac{\sqrt{2}m{v}_{0}}{qB}$,
由几何关系可得:l=$\sqrt{2}$R,则:$\frac{\sqrt{2}m{v}_{0}}{qB}$=$\frac{\sqrt{2}}{2}$l,即:$\frac{m}{qB}$=$\frac{l}{2{v}_{0}}$,
运动时间:t2=$\frac{1}{4}$T=$\frac{1}{4}$×$\frac{2πm}{qB}$=$\frac{πl}{4{v}_{0}}$,
粒子到从P点运动到O点过程所用的时间:t总=t1+t2=(8+π)$\frac{l}{4{v}_{0}}$;
(1)粒子从0点射出时速度为$\sqrt{2}$v0;
(2)电场强度大小为$\frac{m{v}_{0}^{2}}{2ql}$;
(3)磁感应强度大小为$\frac{2m{v}_{0}}{ql}$;
(4)从P点运动到0点所用时间t总为(8+π)$\frac{l}{4{v}_{0}}$.
点评 本题考查了粒子在电场与磁场中的运动,掌握平抛运动的处理方法并能运用到类平抛运动中,粒子在磁场中做匀速圆周运动,能正确的画出运动轨迹,并根据几何关系确定各量之间的关系

| A. | 能就是功,功就是能 | |
| B. | 能量转化的多少可用功来量度 | |
| C. | 做功越多,物体的能就越大 | |
| D. | 外力对物体不做功,这个物体就没有能量 |
| A. | 一直在增大 | B. | 先增大后减小 | C. | 先减小后增大 | D. | 一直在减小 |
| A. | 物体在恒力作用下不可能做曲线运动 | |
| B. | 物体在变力作用下一定做曲线运动 | |
| C. | 做曲线运动的物体所受的力的方向一定是变化的 | |
| D. | 合力的方向与物体速度的方向既不相同、也不相反时,物体一定做曲线运动 |

| A. | I1>I2,U1>U2 | B. | I1<I2,U1<U2 | C. | I1<I2,U1>U2 | D. | I1>I2,U1<U2 |
| A. | 运动的时间t=$\frac{2{v}_{0}}{g}$ | B. | 瞬时速率vt=$\sqrt{5}$v0 | ||
| C. | 水平分速度与竖直分速度大小相等 | D. | 位移大小等于$\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$ |
| A. | 质点在AC段运动的时间为80s | B. | 质点在AC段的平均速度为37.5m/s | ||
| C. | 质点在A点的瞬时速度为17.5m/s | D. | 质点在B点的瞬时速度为47.5m/s |
| A. | 红外传感器 | B. | 生物传感器 | C. | 压力传感器 | D. | 光传感器 |
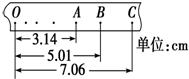 在“验证机械能守恒定律”的实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图(相邻两计数点时间间隔为0.02s),单位 cm,那么
在“验证机械能守恒定律”的实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图(相邻两计数点时间间隔为0.02s),单位 cm,那么