题目内容
5.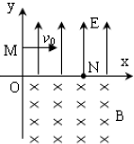 如图所示,在xoy直角坐标平面内,第Ⅰ象限匀强电场沿y轴正方向,第Ⅳ象限匀强磁场垂直于坐标平面向里,质量为m,电量为q的负电粒子,从y轴上的M点(OM=h)以速度v0垂直y轴射入电场,经x轴上的N点(ON=2h)射出电场,进入磁场,最后从y轴上P点(P点未标出)垂直y轴方向射出磁场,不计粒子的重力,求:
如图所示,在xoy直角坐标平面内,第Ⅰ象限匀强电场沿y轴正方向,第Ⅳ象限匀强磁场垂直于坐标平面向里,质量为m,电量为q的负电粒子,从y轴上的M点(OM=h)以速度v0垂直y轴射入电场,经x轴上的N点(ON=2h)射出电场,进入磁场,最后从y轴上P点(P点未标出)垂直y轴方向射出磁场,不计粒子的重力,求:(1)电场强度E的大小;
(2)磁感应强度B的大小.
分析 (1)粒子在第一象限的电场中做类平抛运动,由类平抛运动规律可以求出电场强度.
(2)粒子在磁场中做匀速圆周运动,作出粒子的运动轨迹,由数学知识求出粒子的轨道半径;
洛伦兹力提供粒子做圆周运动的向心力,由牛顿第二定律可以求出磁感应强度.
解答 解:(1)粒子在电场中做类平抛运动,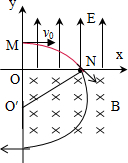
水平方向:2h=v0t1,
竖直方向:h=$\frac{1}{2}$at12=$\frac{1}{2}$$\frac{qE}{m}$t12,
解得:t1=$\frac{2h}{{v}_{0}}$,E=$\frac{m{v}_{0}^{2}}{2qh}$;
(2)粒子进入磁场时的速度:v=$\frac{{v}_{0}}{cos45°}$=$\sqrt{2}$v0,
粒子在磁场中做匀速圆周运动,运动轨迹如图所示,由数学知识可得:
r=$\frac{2h}{cos45°}$=2$\sqrt{2}$h,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
解得:B=$\frac{m{v}_{0}}{2qh}$;
答:(1)电场强度E的大小为$\frac{m{v}_{0}^{2}}{2qh}$;
(2)磁感应强度B的大小为$\frac{m{v}_{0}}{2qh}$.
点评 本题是带电粒子在电场、磁场中运动的综合题,根据题意作出粒子的运动轨迹.应用数学知识求出粒子在磁场中做圆周运动的轨道半径、粒子转过的圆心角,是本题的难点,也是正确解题的关键.

练习册系列答案
相关题目
15. 如图所示,铁饼运动员奋力将质量为m的铁饼以初速度v0抛出,v0与水平面成α角,铁饼到达的最大高度为h,半径空气阻力和抛出点的高度,则运动员抛铁饼过程对铁饼做的功是( )
如图所示,铁饼运动员奋力将质量为m的铁饼以初速度v0抛出,v0与水平面成α角,铁饼到达的最大高度为h,半径空气阻力和抛出点的高度,则运动员抛铁饼过程对铁饼做的功是( )
 如图所示,铁饼运动员奋力将质量为m的铁饼以初速度v0抛出,v0与水平面成α角,铁饼到达的最大高度为h,半径空气阻力和抛出点的高度,则运动员抛铁饼过程对铁饼做的功是( )
如图所示,铁饼运动员奋力将质量为m的铁饼以初速度v0抛出,v0与水平面成α角,铁饼到达的最大高度为h,半径空气阻力和抛出点的高度,则运动员抛铁饼过程对铁饼做的功是( )| A. | $\frac{1}{2}$mv02 | B. | mgh | C. | $\frac{1}{2}$mv02+mgh | D. | mv02+mgh |
16.下列说法正确的是( )
| A. | 布朗运动是液体分子的运动,故分子永不停息地做无规则运动 | |
| B. | 小草上的露珠呈球形的主要原因是液体表面张力的作用 | |
| C. | 自然界中进行的一切宏观过程都具有方向性,是不可逆的 | |
| D. | 当分子间距离为r0时,分子势能最大 |
13.关于分子运动和热现象的说法,正确的是( )
| A. | 布朗运动是指液体或气体中悬浮微粒的运动 | |
| B. | 气体的温度升高,每个气体分子运动的速率都增加 | |
| C. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能不变 | |
| D. | 空调机作为制冷机使用时,将热量从温度较低的室内送到温度较高的室外,所以制冷机的工作不遵守热力学第二定律 |

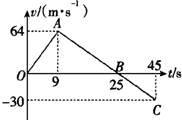 一宇宙空间探测器从某星球表面垂直升高,发动机提供恒力,其质量为M=1500kg,开动一段时间后关闭,根据如图所示v-t图线,求:
一宇宙空间探测器从某星球表面垂直升高,发动机提供恒力,其质量为M=1500kg,开动一段时间后关闭,根据如图所示v-t图线,求: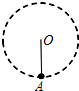 如图所示,长为1m的轻绳,一端系着一质量为2kg的小球,以O为圆心,在竖直平面内做圆周运动,小球通过最高点的速度为4m/s,则小球通过最低点时对绳子的拉力为(g取10m/s2)( )
如图所示,长为1m的轻绳,一端系着一质量为2kg的小球,以O为圆心,在竖直平面内做圆周运动,小球通过最高点的速度为4m/s,则小球通过最低点时对绳子的拉力为(g取10m/s2)( )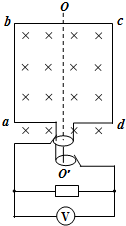 如图所示,为一交流发电机和外接负载的示意图,发电机电枢线圈n=100匝的矩形线圈,边长ab=ad=L=0.2m,绕OO′轴在磁感强度B=$\frac{2}{π}$T的磁场中以角速度ω=300R/min转动(不计摩擦),线圈总电阻r=1Ω,外电路负载电阻R=9Ω.试求:
如图所示,为一交流发电机和外接负载的示意图,发电机电枢线圈n=100匝的矩形线圈,边长ab=ad=L=0.2m,绕OO′轴在磁感强度B=$\frac{2}{π}$T的磁场中以角速度ω=300R/min转动(不计摩擦),线圈总电阻r=1Ω,外电路负载电阻R=9Ω.试求: